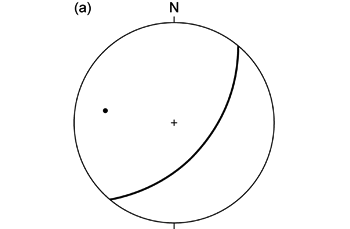
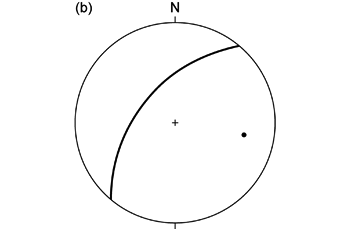
球面投影 (spherical projection) は球面を平面に投影する方法の 1 つである。 球面上の位置情報は三次元だから，それを紙のような二次元の平面上で表すためには，何らかの投影法が必要となる。 身近な例を挙げると，世界地図は地球表面を平面上に表したものであり，さまざまな投影法が考案されていることはよく知られている。 球面投影はこのような投影法の 1 つで，紀元前から天文学をはじめとする多くの分野で使われてきたらしい (Howarth, 1996)。

地質学では様々な線や面を扱う。 地質学で扱うこれらの線・面は，多くの場合，直線・平面だと考えて構わない。 そこで以後特に断らない限り (おそらく断ることはないが) 直線と平面だけを考え， 線・面とはそれぞれ直線・平面を意味するものとする。 なお，この後の解説では様々な直線・平面が登場するが，説明をできるだけわかりやすくするために， 投影の対象となる直線・平面は線・面と書き，それ以外については直線・平面と書いて区別するようにする。

地質学で一般に用いられる球面投影には等角投影 (equal-angle projection) と 等積投影 (equal-area projection) の 2 種類がある ( 1.3. )。 地質学でおこなう等角投影と等積投影は，投影法が似ており，またステレオネット ( 第 2 章 ) を使えば投影操作は基本的に同じなので， 地質学の分野では (少なくとも日本では) 等角・等積両方の投影をあわせてステレオ投影と呼ぶことが少なくないようである。 ただし，厳密に言えばステレオ投影 (stereographic projection) とは等角投影のみを指す。 なお，地質学実験ではすべて等角投影を用いて実習をおこなう。

地質学における球面投影では，仮想球体の中心を通る線や面と仮想球体表面との交点・交円 ( 図 1.1.1. ) を投影面に投影する。 この中心を通るという点は重要なので忘れないようにしたい。

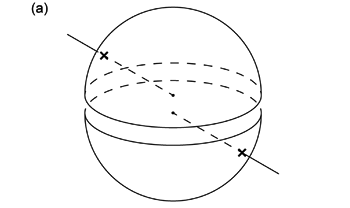
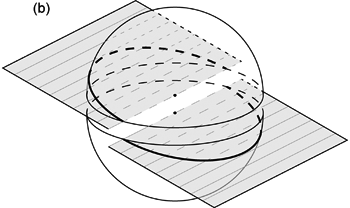
仮想球体の中心を通る線は仮想球体表面と 2 点で交わる ( 図 1.1.1. a )。 このとき 2 つの交点の位置は球の中心に関して対称である。 また球の中心を通る面は，球面と円で交わる ( 図 1.1.1. b )。 この交円は仮想球体の中心を中心とする円だから，やはり球の中心に関して対称だと言える。 だとすれば，仮想球体を，中心を通る平面で2つの半球に分けても， 球面と線・面との交点・交円は，両方の半球で球の中心に関して対称な位置にあるはずである ( 図 1.1.2. )。 このことは地質学的な球面投影を理解する上で重要である。 なぜなら地質学で考える球面投影では，この性質を利用して，どちらか一方の半球だけを投影するからである。 このように半球だけを投影することを半球投影 (hemispherical projection) と呼ぶ。

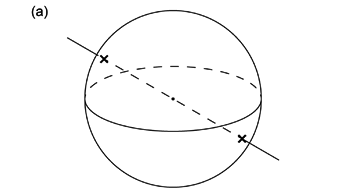
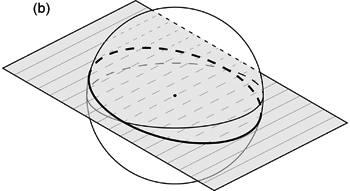
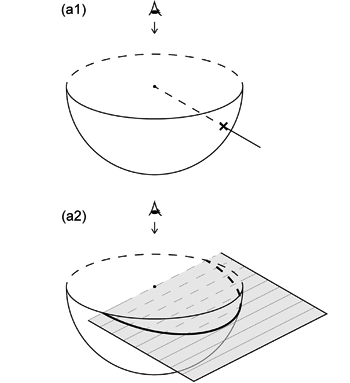
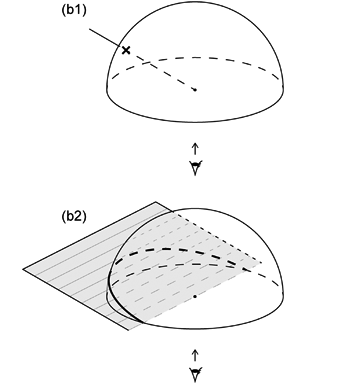
半球投影では，投影面と平行な面で球体を 2 つの半球に分ける。 そのときどちらか一方の半球だけを考えれば，中心を通る線は普通その半球とは 1 点で交わる ( 図 1.1.2. a )。 したがって半球投影ではこの 1 点が投影面に投影される。 ただし線が投影面と平行な場合のみは，どちらの半球の投影でも 2 つの交点両方が投影されることになる。 また面の場合，半球とは普通半円で交わる ( 図 1.1.2. b )。 そこで半球投影ではこの半円が投影される。 そして面が投影面と平行な場合のみ，どちらの半球の投影であっても半円でなく円が投影される。 そのときその円は投影面上でも円となる。 半球投影では，この投影面と平行な面が投影された円のことを基円 (primitive circle) と呼ぶ。 なお， 1.3.1. や 1.3.4. の投影原理を見ればわかるように， 半球投影では，半球上のどの位置であっても基円よりも外側に投影されることはない。

地質学では通常は投影面を水平にとるから，仮想球体は上下 2 つの半球に分けられることになる。 このとき上半球と線・面との交点・交円を投影することを上半球投影 (upper hemisphere projection)，下半球と線・面との交点・交円を投影することを下半球投影 (lower hemisphere projection) と呼ぶ。 先に述べたように線と球面との交点の位置は球体の中心に関して対称だから， どちらの半球を投影するかによって，投影面上で線の投影される位置は異なる ( 図 1.1.3., 1.1.4. )。 したがって，半球投影を用いた際は， どちらの半球を投影したのか (投影面を水平にとったなら上半球投影したのか下半球投影したのか) を明らかにしておく必要がある。

半球投影では，どちらの半球を投影するかによって視点の位置が異なると考えれば良い。 例えば上半球投影であれば仮想球体の底点に視点をおいた投影をおこない，下半球投影の場合は頂点に視点をおいた投影をおこなう ( 図 1.1.3. )。 しかし視点と投影する半球が異なる以外両者に違いはなく，どちらの半球を投影するかは自由に選ぶことができる。

地質学の場合，線がプランジする・面が傾斜するとは， 線・面が水平から下方へ傾いていることを意味する。 またプランジ方向・傾斜方向とは線・面が水平から下方へ傾いていっている方向のことである。 だから下方へ傾く線・面が，下半球と交わる点・半円を投影するほうが感覚的にも視覚的にも理解しやすい ( 図 1.1.4. )。 下半球投影を使えば，例えば東側へプランジする線・傾斜する面は下半球の東側部分で半球と交わり， 投影面においても東側に投影される。 一方で上半球投影を使うと，これらの線・面は西側に投影されることになる。 どちらも同義なのだが，下半球投影のほうが直観的に理解しやすいことはわかるだろう。 そのため地質学では通常下半球投影が用いられる。 地質学実験では下半球投影のみを使う。 しかしどちらの半球の投影であっても基本的に同じことである。