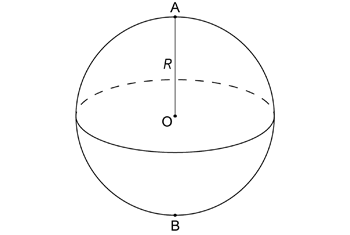
球面投影
1. 球面投影の原理
1.3. 等角投影・等積投影
地質学では等角投影と等積投影がよく用いられることは既に述べた。 球面投影では球面を平面で表そうというのだから,すべてそのままというわけにはいかず, 何かを正しく投影しようと思えば,どうしても他の何かを犠牲にしなければならなくなる。 球面上での角度を正しく投影しようとするのが等角投影であり,面積を正しく投影しようとするのが等積投影である。 等角投影では面積は基本的に保存されないし,等積投影では角度は基本的に保存されない。
地質学的な目的で球面投影する場合,基本的には等角・等積どちらの投影法を用いておこなっても構わない。 両者は投影面上で何が保存されているかが異なるだけだからである。 しかし投影目的によっては,いずれかの投影法を用いるべきだということはある ( 図 1.3.1. )。 例えば,何かが定向配列していることを球面投影を使って示したい場合, それぞれの向きを線として球面投影すれば良いが, その場合は球面上の単位面積あたりの頻度で示したほうがわかりやすいから,等積投影を用いるべきである。
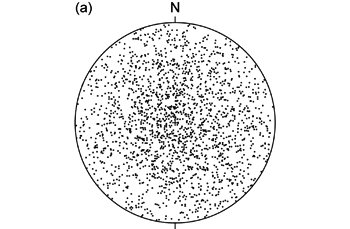
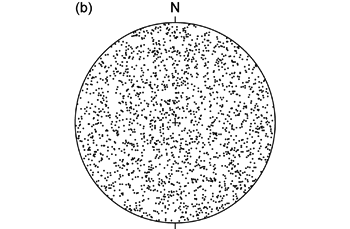
等角投影や等積投影がどういうものかは小学校などでよく習う地図を思い出せば理解しやすい。 例えばメルカトル図法 (Mercator projection) では角度は保存される (だから経線と緯線はかならず直交する) が, 高緯度地域が相対的に引き伸ばされて面積は保存されない。 一方モルワイデ図法 (Mollweide projection) では面積は保存されるが角度は保存されない。 これらの図法の投影法は球面投影とは全く異なるが, 何かしら妥協することによって球面を平面に投影している点では球面投影と同じである。 ここで扱う球面投影と同様の投影法を使っている地図法には, 等角投影では平射図法 (stereographic projection,この場合は等角投影と同義), 等積投影ではランベルト正積方位図法 (Lambert azimuthal equal-area projection) がある。
次に等角投影・等積投影の原理をそれぞれ説明する。 投影原理上,投影面の姿勢は問題ではないが,以下では説明をわかりやすくするために,投影面は水平面とする。 また仮想球体が繰り返し出て来るが,ここではすべて球体の中心を \(\mathrm{O}\),半径を \(R\) とし, 投影面に対する上半球側の頂点を \(\mathrm{A}\),下半球側の底点を \(\mathrm{B}\) とする ( 図 1.3.2. )。 このとき直線 \(\mathrm{AB}\) は投影面の法線となる。 説明は下半球投影を例とするが,上半球投影であっても原理は同じである。