球の中心を通る面が球面と円で交わることは上で見た通りである ( 図 1.2.1. a )。 このような球の中心を通る面と球面との交円を大円 (great circle) と呼ぶ。 半球投影では，面が投影面と平行でなければ，大円の半分である半円が投影される。 この半円は大円を代表するものであるから，やはり大円と呼ばれる。 またその半円が投影された曲線もまた，大円を投影したものであるから，大円と呼ばれる。 面が投影面と平行な場合のみ大円は円として投影され，それが基円である。 上で述べたように，地質学でおこなう球面投影では，面は必ず球の中心を通るものとして投影される。 したがってこのときの面と球面との交円は常に大円である。

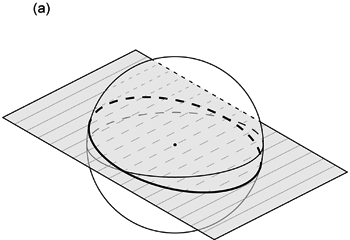
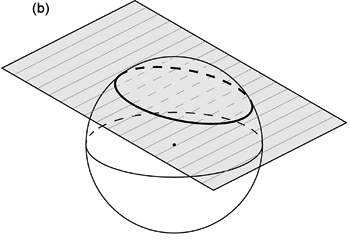
一方で球の中心を通らない面も球面と円で交わる ( 図 1.2.1. b )。 この中心を通らない面と球面との交円を小円 (small circle) と呼ぶ。 小円は必ず大円よりも小さい。 また小円は中心を通らない面と球面との交円であるから，2 つの半球で対称だとは限らない。

小円はまた，球体の中心を通る線 \(\mathrm{L}_1\) を回転軸とし， その線に対して斜交する線 \(\mathrm{L}_2\) (球体の中心で \(\mathrm{L}_1\) と交わる) を回転させたときの， \(\mathrm{L}_2\) と球面との交点の軌跡と言い換えることもできる ( 図 1.2.2. )。 製図用のコンパス (円を描くために使用されるコンパス) を考えてみよう。 コンパスの 2 本の足を少し開いて，片方の足を軸に回転させてみる。 それを，軸にしている足の先端側から見れば，もう一方の足の先が円を描いているのがわかる。 コンパスの足の長さと同じ半径の球体を考え，2 本の足の交点を球体の中心に置けば， 回転している足の先端は (2 本の足の長さが同じであれば) 必ず球面上にある。 つまりその足の先と球面との交点の軌跡は円になるのである。 この考え方は，ステレオネットを使った回転操作で使うから，理解しておく必要がある。

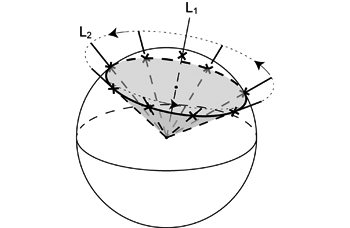
またこのとき，回転する線 \(\mathrm{L}_2\) 自体の軌跡は円錐になる。 したがって小円は，頂点を球体の中心とする円錐と球面との交円であるということもできる。 このことを利用して円錐を投影することもできる (円錐の投影については実習の手引き参照)。 なお，回転軸と直交する線と球面との交点の軌跡は大円になる。