球面投影
1. 球面投影の原理
1.3. 等角投影・等積投影
1.3.1. 等角投影の原理
等角投影では角度が保存される。 つまり仮想球体表面にあり，球面上の任意の点で交わる 2 つの直線のなす角は，投影されてもそのままの角度を保つ。 もっとわかりやすく言えば，球体表面にある形が (十分小さければ)，投影後もそのままの形で保存されるということである。
地質学でよく用いられる等角投影では仮想球体の中心を通る水平面を投影面とする。 下半球投影であれば，仮想球体の底点 \({\rm B}\) における球体の接平面を投影面と考えることもできる (上半球投影なら頂点 \({\rm A}\) における接平面)。 その場合は後で説明する等積投影と同じ投影面のとり方ということになる ( 1.3.4. )。 どちらにしても基本的には同じことであるが，中心を通る平面としたほうが， 投影作業の際にイメージしやすいように思うので，ここではまず中心を通る平面を投影面として説明し， 最後に底点 \({\rm B}\) における球体の接平面を投影面とした場合について説明する。
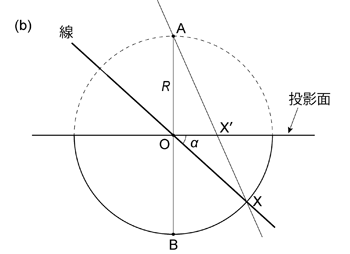
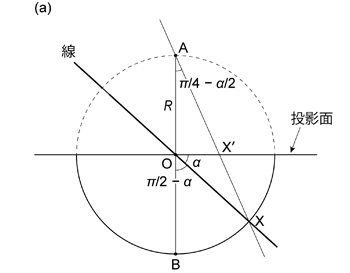
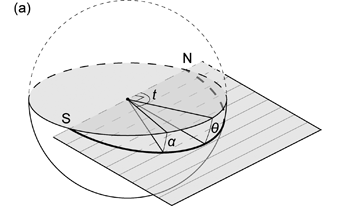
上で述べたように線を球面投影するということは，線と仮想球体との交点を投影面に投影することである。 また投影される線は必ず仮想球体の中心 \({\rm O}\) を通る。 \({\rm O}\) を通り仮想球体の下半球と点 \({\rm X}\) で交わるような線 \({\rm OX}\) は， 直線 \({\rm AX}\) と投影面との交点 \({\rm X}'\) に投影される ( 図 1.3.3. )。 これが下半球等角投影の基本的な考え方である。 この場合 \({\rm A}\) 点を視点としているわけで，面や線を真上から見ていると考えれば良い。 上半球投影の場合は上下が逆になるだけのことである。
具体的な投影位置について考えてみよう。 トレンドが \(t\)，プランジが \(\alpha\) (トレンド・プランジについては実習の手引き参照) の線 \({\rm L}\) を水平な投影面に下半球投影する。 ここでは簡単にするためトレンドは線のプランジしている方向として， アジマス (上から見て北から時計回り \(360^\circ\) の角度) で考えよう。 角度をラジアンで表せば，\(0 \le t \lt 2\pi\) であり，\(0 \le \alpha \le \pi/2\) である。 下半球等角投影では，上で述べたように，線 \({\rm L}\) と仮想球体の下半球との交点 \({\rm X}\) は 投影面上の点 \({\rm X}'\) に投影される ( 図 1.3.3. )。 基円の半径 (この投影の場合は仮想球体の半径 \(R\) に等しい) を \(r\) とすると， 基円の中心 (すなわち仮想球体の中心 \({\rm O}\)) と \({\rm X}'\) との距離 \(O{X'}\)は
\begin{align} OX' & = R \tan \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) = \frac{R \cos \alpha}{1 + \sin \alpha}\\ \nonumber & = r \tan \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) = \frac{r \cos \alpha}{1 + \sin \alpha} \tag{1.3.1} \end{align}
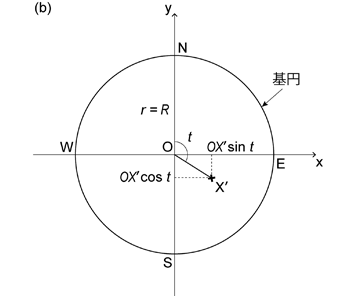
で求められる ( 図 1.3.4. a )。 投影面上で基円の中心を原点とし，東西方向を \(x\) 軸，南北方向を \(y\) 軸とする直交座標を考えると (それぞれ東向き，北向きを正としておく)，\({\rm X}'\) は
\begin{align} x = OX' \sin t , \tag{1.3.2} \end{align}
\begin{align} y = OX' \cos t \tag{1.3.3} \end{align}
に投影されることになる (図 1.3.4. b )。
また，\(\alpha = 0\) すなわち水平な線は，基円上に投影される。 その際水平な線は，基円上の (\(r \sin t\), \(r \cos t\)) だけでなく， それと基円の中心に関して対称な位置 (\(-r \sin t\), \(-r \cos t\)) の 2 点に投影されることに注意しなければならない。 線が投影面と平行な場合のみ，線は半球と 2 つの交点をもつからである。 これらのことからわかるように，下半球面上のあらゆる点は基円とその内側に投影される。
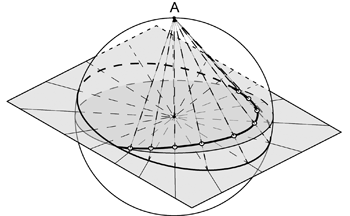
では次に面 \({\rm P}\) の投影を考える。 簡単にするため面の姿勢は南北走向で，傾斜角 \(\theta\) で東傾斜しているとし (走向と傾斜については実習の手引き参照)，水平な投影面に下半球投影する。 このとき \(0 \le \theta \le \pi /2\) である。 線の場合と同様に面 \({\rm P}\) は仮想球体の中心を通る。 したがって面 \({\rm P}\) と仮想球体表面の交円は大円となる。 また面 \({\rm P}\) が傾斜していれば (\(0 \lt \theta \le \pi /2\))， 面は仮想球体の下半球表面とは半円で交わるから，面 \({\rm P}\) を球面投影するためには， この半円を大円を代表するものとして投影面に投影すれば良い。 なお面 \({\rm P}\) が水平な場合 (\(\theta = 0\)) のみは大円は円として投影され， それが基円になる。
さて面 \({\rm P}\) は，仮想球体の中心を通り面 \({\rm P}\) 上にある直線の集合として考えることもできる ( 図 1.3.5. )。 したがって投影される大円は，そのような直線と仮想球体表面との交点の集合である。 ではこれらの交点は，投影面上のどのような位置に投影されるだろうか。
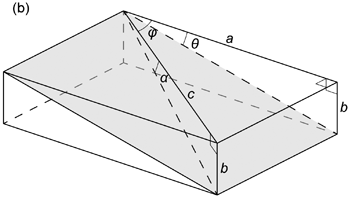
線は 式 (1.3.1)， (1.3.2)， (1.3.3) よりトレンドとプランジがわかれば投影できる。 だから面 \({\rm P}\) 上にありトレンドが \(t\) の線 \({\rm L}\) のプランジ \(\alpha\) を求められれば， 線 \({\rm L}\) の投影は可能である。 あとは面 \({\rm P}\) が南北走向なので， \({\rm L}\) のトレンドを \(0\) から \(\pi\) まで変化させれば 面 \({\rm P}\) の投影ができることになる。 面 \({\rm P}\) が南北走向で東傾斜だということは， 傾斜方向のトレンド (傾斜方向は線として考えられる) は \(\pi /2\) である (面の傾斜方向は走向に直交する)。 したがって面 \({\rm P}\) の傾斜方向のトレンドと線 \({\rm L}\) のトレンドとがなす角は \(| \: t - \pi /2 \: |\) となる。 \(0 \le \theta \lt \pi/2\) のとき， 図 1.3.6. b のような関係を考えれば，\(b/c = b/a \times a/c\) であることから，
\begin{align} \tan \alpha & = \tan \theta \cos \left( \left| \: t - \frac{\pi}{2} \: \right| \right) \\ \nonumber & = \tan \theta \sin t \tag{1.3.4} \end{align}
という \(t\) と \(\alpha\) の関係がわかる。 したがって \(0 \le \theta \lt \pi/2\) であるような面 \({\rm P}\) はトレンド \(t\) (\(0 \le t \le \pi\))， プランジ \(\alpha = \tan^{-1} (\tan \theta \sin t)\) の線の集合として投影できる。 それぞれの \(t\) のときの投影位置 \((x,~y)\) は 式 (1.3.1)， (1.3.2)， (1.3.3) を用いて求められるだろう。
面 \({\rm P}\) が鉛直 (\(\theta = \pi /2\)) であれば， 面 \({\rm P}\) 上にあるあらゆる線のトレンドは面の走向に等しく，\(0 \le \alpha \le \pi /2\) で考えるなら， \(t = 0\) および \(t=\pi\) となる (面 \({\rm P}\) は北にプランジした線と南にプランジした線の集合であるため)。 したがって面 \({\rm P}\) は \(t = 0\) および \(t=\pi\) で \(0 \le \alpha \le \pi /2\) の線の集合として投影され， 投影面上には基円上の 2 点，\(t = 0\)， \(\alpha =0\) の投影点 (\(0\), \(r\)) と \(t = \pi\)， \(\alpha = 0\) の投影点 (\(0\), \(-r\)) を結ぶ線分 (以下この線分を直線状の大円と呼ぶ) として投影される。
面 \({\rm P}\) が西傾斜であっても同じことである。 簡単に考えるなら，上とは逆に，西向き，南向きをそれぞれ \(x\) 軸，\(y\) 軸の正とし， \(t\) は南を起点とするアジマスとすれば，上と全く同じになる。 また面の走向が南北でなければ，走向線 (面と水平面との交線) を \(y\) 軸とし， それと直交する方向に \(x\) 軸 (面の傾斜方向を正とする) をとれば，同様に考えられる。
先に，等角投影では投影面を仮想球体上の 1 点における球体の接平面にとることもあり， それでも中心を通る平面を投影面とする場合と同じことだと述べた。 最後にそのことについても確認しておこう。
仮想球体の底点 \({\rm B}\) における水平な仮想球体の接平面を投影面とする下半球投影を考える (上半球投影では球の頂点 \({\rm A}\) における接平面を投影面とする)。 この投影では，仮想球体の中心 \({\rm O}\) を通り仮想球体の下半球と点 \({\rm X}\) で交わるような線 \({\rm OX}\) は， 直線 \({\rm AX}\) と投影面との交点 \({\rm X}'\) に投影される ( 図 1.3.7. )。 このとき，基円の半径 \(r\) は仮想球体の直径に等しく \(r = 2R\) である。
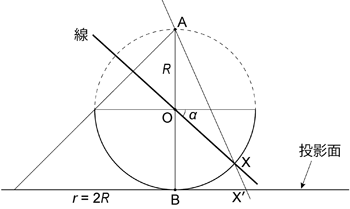
トレンドが \(t\)，プランジが \(\alpha\) の線 \({\rm L}\) を下半球投影することを考えてみよう。 基円の中心 (すなわち仮想球体の底点 \({\rm B}\)) と \({\rm X}'\) との距離 \(B{X'}\) は
\begin{align} BX' = 2R \tan \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) = \frac{2R \cos \alpha}{1 + \sin \alpha} \tag{1.3.5} \end{align}
である。ここで \(r = 2R\) だから，この式は
\begin{align} BX' = r \tan \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) = \frac{r \cos \alpha}{1 + \sin \alpha} \tag{1.3.6} \end{align}
と書き換えることができる。 つまり基円の中心 \({\rm B}\) と \({\rm X}'\) との距離 \(B{X'}\) は，基円の半径を用いて表すなら， 式 (1.3.1) と同じなのである。 投影する際は基円の半径だけが問題となるから，このことはつまり， いずれの方法で投影面をとっても，投影位置は同じであることを意味している。 面は線の集合として考えることができるから，面についても， やはり投影面を仮想球体の中心を通る平面にとったときと同じことである。 したがって，投影面を，仮想球体の中心を通る平面としても， 仮想球体上の 1 点における球体の接平面としても，まったく同じことである。