前章 1.3.1. と 1.3.4. で見たように， 等角・等積いずれの投影でも，トレンド \(t\)，プランジ \(\alpha\) の線は， 水平な投影面上で基円の中心 \({\rm O}\) を原点とし (ここでは \({\rm O}\) を基円の中心としていることに注意)， 東西方向を \(x\) 軸，南北方向を \(y\) 軸とする直交座標を考えたとき (それぞれ東向き，北向きを正とする)， \(x = OX' \sin t\)，\(y = OX' \cos t\) となる点 \({\rm X'}\) に投影される。 また基円の半径を \(r\) とすれば，等角投影では \(OX' = r \tan (\pi /4 - \alpha/2)\) であり， 等積投影では \(OX' = r \: \sqrt[]{1 - \sin \alpha}\) である。 面は線の集合として投影できることもわかった。 しかし，手作業で投影しようとする場合，これらを計算して投影位置を求め， さらに紙の上でその投影位置に正しくプロットするというのは現実的ではない。

そこで手作業での投影の際に用いられるのがステレオネット (stereonet) である ( 図 2.1.1. )。 ステレオネットには，あらかじめ球面と複数の面との交円を投影した曲線や線分が描かれてあるので， それらの曲線・線分は何が投影されたものなのかさえ理解すれば， それらや，それら同士の交点を手掛かりにして，複雑な計算をすることなく， 自分の投影したい線・面の投影位置を決められる。 つまりステレオネットは特殊な方眼紙のようなものだと考えれば良い。 方眼紙の升目は距離を表しているが，ステレオネットの升目 (のようなもの) は角度を表している。

ステレオネットは投影を補助するための役割のものであって， ステレオネット自体に方位はない。 ステレオネットに方位 (N や S) を記入しているものをしばしば目にするが (構造地質系の某教科書など)， ステレオネットの使用目的を考えると，これは明らかな間違いである。 おそらく大円群と小円群の関係を地球儀の経線・緯線の関係で理解しやすくしようという意図があって， 故意にそうしているのではないかと思われるが，ステレオネットを正しく理解するためには，方位は記入すべきでない。

些細な問題のように思われるかもしれないが，実習で方位の記入されていないステレオネットを使っていても， しばしばステレオネットに方位があるかのように勘違いし，そのせいで投影操作が正しくできていない例は少なくない。 ステレオネットに方位はないということは，ステレオネットを用いた投影を理解するために，実はかなり重要な点なのである。

投影法に等角・等積の 2 種類あり，球面上の同じ点でもそれぞれ投影位置が異なることからわかるように， ステレオネットには等角投影用のものと等積投影用のものがある。 先に述べたように球面投影とは厳密には等角投影を指すから， ステレオネットも正しくは等角投影用のものを指すと考えられるが， ここではやはり等角・等積両方を含めてステレオネットと呼ぶことにする。 地質学の分野では等角投影用のものはウルフネット (Wulff net)， 等積投影用のものはシュミットネット (Schmidt net) と呼ばれるのが一般的である ( 図 2.1.1. )。

ステレオネットに描かれているのは，一般に大円と小円である。 既に見たように，大円とは，球体の中心を通る平面と球面との交円のことである。 例えば地球儀の経線は地球の自転軸を含む大円である。 一方小円は球体の中心を通らない平面と球面との交円のことで， 例えば地球儀の緯線は地球の自転軸と直交する方向の小円 (赤道だけは大円) となっている。 地質学では通常半球投影を用いるからステレオネットに描かれている大円・小円はいずれも半球分のものである。

ウルフネットとシュミットネットにはさらに，両方に共通した複数の種類がある。 よく使われるのは 2 種類で，equatorial net と呼ばれるものと polar net と呼ばれるものである ( 図 2.1.1. )。 equatorial net と polar net の統一的な訳語は不明なので， 以下それぞれ赤道投影ネット (equatorial net) および極投影ネット (polar net) と呼ぶ。 なお赤道投影ネットは狩野・村田 (1998) が子午線投影網 (meridional net) と呼んでいるものと同じものである。

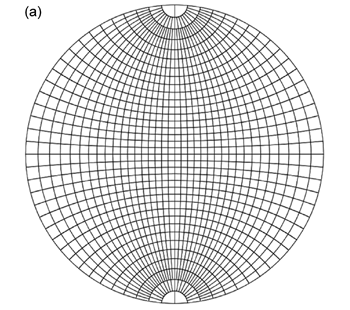
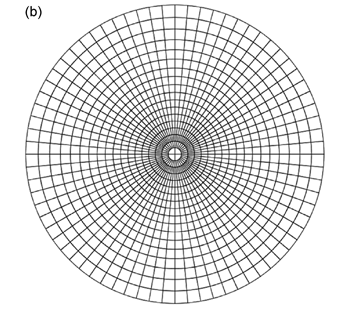
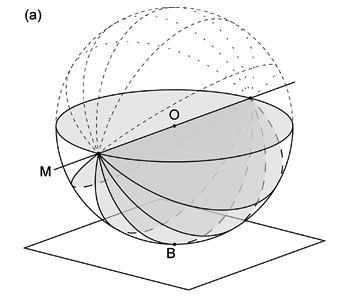
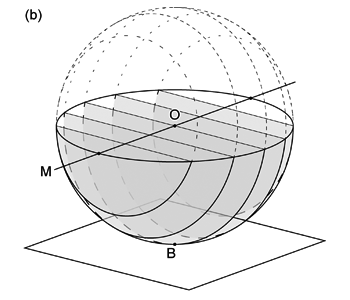
赤道投影ネットは基円の他に，(1) 投影面と平行で球体の中心 \({\rm O}\) を通る直線 (ここでは直線 \({\rm M}\) としよう) を含む平面と球面との交円 (大円; 図 2.1.2. a )， (2) \({\rm M}\) を法線とするような平面と球面との交円 (小円・大円; 図 2.1.2. b )，の両方を投影した曲線を描いたものである。 上で地球儀の経線は地球の自転軸を含む大円であり，経線は自転軸と直交する方向の小円・大円であると述べたが， 自転軸を直線 \({\rm M}\) と考えれば，赤道投影ネットとは投影面を， 自転軸を含む平面あるいは地球表面の赤道上の 1 点における接平面にとり，経線・緯線を半球分投影したものということになる。

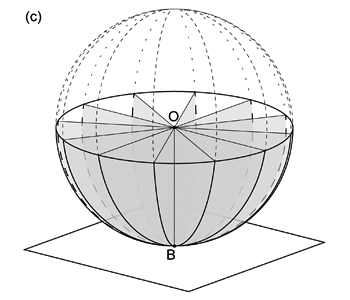
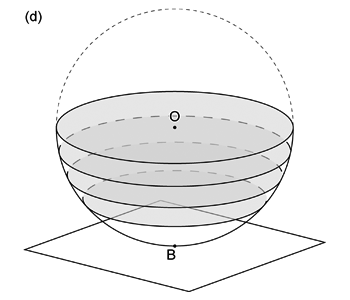
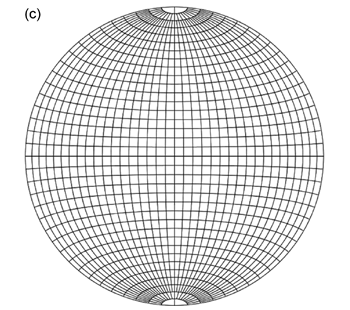
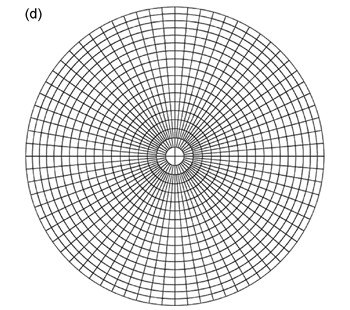
極投影ネットは基円のほかに，(1) 球の中心を通り投影面と垂直な平面と球面との交円 (大円; 図 2.1.2. c ) と， (2) 投影面と平行な平面と球面との交円 (小円・大円，ただし大円の場合はそれが基円; 図 2.1.2. d )， の両方を投影した線分 (大円) と円 (小円) を描いたものである。 再び地球儀でいえば，投影面を赤道面 (ウルフネット) あるいは北極もしくは南極点における接平面 (シュミットネット) にとり， 経線・緯線を半球分投影したものである。

地球儀の経線・緯線を例に考えると，赤道投影ネットと極投影ネットとは，投影面の位置まで異なる， かなり違ったもののように思われるかもしれないが，ステレオネットは地球や地球儀を投影したものではなくて， もっと一般的なものであるから，両者に大きな違いはない。 ステレオネットには地球の経線や緯線が描かれているわけではないことに注意したい。 赤道投影ネットと極投影ネットとの違いは，ただ描かれている曲線・線分の種類が違う， つまり投影されている面と投影面との関係が異なっているというだけのことである。 これは投影目的によって，どんな面の投影されたステレオネットが使いやすいかが異なるからである。 例えば面を大円で投影するような場合には赤道投影ネットが便利だし， 面を極のみで投影する場合には極投影ネットの方が便利な場合がある (それぞれの投影法については実習の手引き参照)。