等積投影の原理も等角投影のそれと基本的にはよく似ている。 だから等角投影の原理を理解していれば，等積投影の原理も理解しやすいだろう。 しかし逆に，似ているから混同しないようにしたい。

下半球等積投影では仮想球体の底点 \({\rm B}\) における仮想球体の接平面を投影面とする。 したがって \({\rm B}\) が基円の中心となる。 \({\rm O}\) を通り仮想球体の下半球と点 \({\rm X}\) で交わるような線 \({\rm OX}\) は， 直線 \({\rm AX}\) と投影面との交点を \({\rm Y}\) としたときに， 半直線 \({\rm BY}\) 上において \(BX = BX'\) となるような \({\rm X'}\) に投影される ( 図 1.3.16. )。 上半球投影の場合は上下が逆になり，したがって投影面は頂点 \({\rm A}\) における仮想球体の接平面となるが， 考え方は同じである。 またここでは投影面を水平面として説明しているが，原理としては， 等角投影と同様に投影面は必ずしも水平である必要はない。

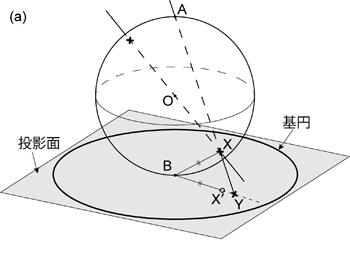
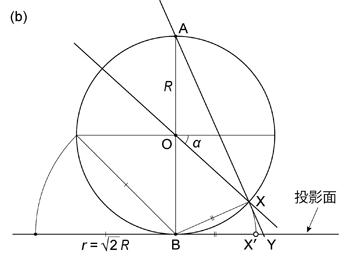
この投影では，投影面と平行で仮想球体の中心を通る面が仮想球体と交わる大円は，半径 \(r = \sqrt[]{2}R\) の円として投影される ( 図 1.3.16. b )。 そしてこれが基円となる。 等角投影とは，底点 \({\rm B}\) における仮想球体の接平面を投影面とした場合とも， 基円の半径が (より正確に言うなら仮想球体の半径と基円の半径との関係が) 異なっている。 ただし，もちろん \(R\) はあくまでも「仮想」球体の半径だから， 等角投影と等積投影とで基円の半径を変えなければならないわけではない。

ではまた具体的な投影位置について考えよう。 等角投影のときと同じくトレンドが \(t\)，プランジが \(\alpha\) の線 \({\rm L}\) を水平な投影面に下半球投影してみる。 トレンドはやはり線のプランジしている方向としてアジマスで考え，\(0 \le t \lt 2\pi\)，\(0 \le \alpha \le \pi/2\) である。 下半球等積投影では，上で述べたように，線 \({\rm L}\) と仮想球体の下半球との交点 \({\rm X}\) が， 直線 \({\rm AX}\) と投影面との交点を \({\rm Y}\) として， 半直線 \({\rm BY}\) 上において \(BX = BX'\) となるような \({\rm X'}\) に投影される ( 図 1.3.16. )。 そのとき基円の中心 (すなわち仮想球体の底点 \({\rm B}\)) と \({\rm X'}\) との距離 \(B{X'}\) は，

\begin{align} BX' = 2R \sin \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) \tag{1.3.20} \end{align}

となる。 \(BX'\) は正であることを考えれば，

\begin{align} BX' = R \: \sqrt[]{2(1 - \sin \alpha)} \tag{1.3.21} \end{align}

であり，また基円の半径 \(r = \sqrt[]{2}R\) だから，

\begin{align} BX' = r \: \sqrt[]{1 - \sin \alpha} \tag{1.3.22} \end{align}

として基円の大きさで表すことができる。 等角投影の場合と同様に，投影面上で基円の中心を原点とし，東西方向を \(x\) 軸， 南北方向を \(y\) 軸とする直交座標を考えると (それぞれ東向き，北向きを正とする)，\({\rm X'}\) の投影位置は 式 (1.3.2)， (1.3.3) と同様に，

\begin{align} x = BX' \sin t, \tag{1.3.23} \end{align}

\begin{align} y = BX' \cos t \tag{1.3.24} \end{align}

となる。 また水平な線 (\(\alpha = 0\)) が基円上の \((r \sin t,~r \cos t)\) および \((-r \sin t,~-r \cos t)\) の 2 点に 投影されるのも等角投影と同様であり， やはり下半球面上のあらゆる点は基円とその内側に投影される。

面の投影についても，等角投影の時と同様に線の集合で考えれば良い。 南北走向で東に \(\theta\) 傾斜する面 \({\rm P}\) は，\(0 \le \theta \lt \pi/2\) であればトレンド \(t\) \((0 \le t \le \pi)\) プランジ \(\alpha = \tan^{-1} (\tan \theta \sin t)\) の線の集合として 式 (1.3.21)， (1.3.23)， (1.3.24) を利用して投影できるし， \(\theta = \pi /2\) であれば，\(t = 0\) および \(t=\pi\) で \(0 \le \alpha \le \pi /2\) の線の集合として投影できる。 もちろん任意の姿勢の面がこの考え方を使って投影できるのも等角投影と同様である。