球面投影
2. ステレオネット
2.1. ステレオネットの種類
2.1.1. 赤道投影ネット
地質学実験ではウルフの (等角投影用の) 赤道投影ネットを使う。 そこで赤道投影ネットについてもう少し詳しく説明しておく。 上で述べたように赤道投影ネットには,投影面と平行な直線 \(\mathrm{M}\) を含む平面と球面との交円 (大円) が描かれている ( 図 2.1.2. a )。 地図で言うところの経線のように見える線がそれである ( 図 2.1.1. a, c )。 これらは大円が投影されたものだから,ステレオネット上でも大円と呼ばれる。 以下説明のためにこれらの大円をまとめて「大円群」と呼ぼう ( 図 2.1.3. a )。
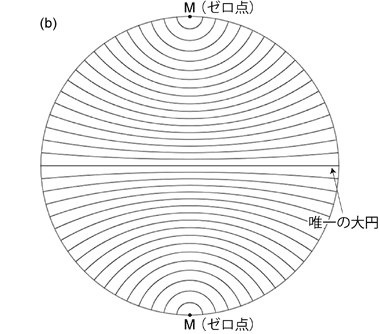
さらに赤道投影ネットには直線 \(\mathrm{M}\) を法線とするような平面と球面との交円 (小円と大円) も描かれている ( 図 2.1.2. b )。 面が中心を通った場合のみが大円なので,大円は 1 つだけである。 これらも,ステレオネット上でも小円・大円と呼ばれる。 こちらの大円は小円の特殊な場合であると考えれば良いから,これらをまとめて「小円群」と呼ぶことにする ( 図 2.1.3. b )。 地図で言うところの緯線のように見える線がそれであり,赤道のように見えるものだけが大円である ( 図 2.1.1. a, c )。 地質学実験で配布するステレオネットはウルフネットだが,赤道投影ネットであれば,ウルフネットでもシュミットネットでも, 投影法が異なるだけで投影されている面の種類は同じであり,基本的に同じように使うことができる。
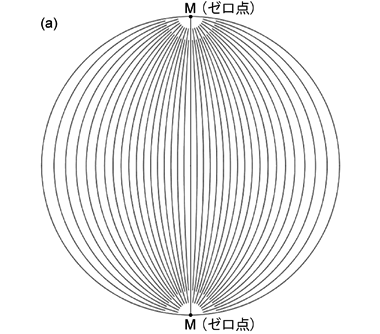
赤道投影ネット ( 図 2.1.1. a, c,または実習で配布されたもの) を見てみよう。 基円上の 2 点を結ぶ曲線がたくさん描かれているが,これが大円群である。 このときその基円上の 2 点が,上でいう直線 \(\mathrm{M}\) が投影された位置である (直線 \(\mathrm{M}\) は投影面と平行だから基円上の 2 点に投影される)。 説明を簡単にするためにこれらの 2 点を以下「ステレオネットのゼロ点」あるいは単に「ゼロ点」と呼ぶことにしよう ( 図 2.1.3. )。 数字の \(\mathrm{0}\) はアルファベットの \(\mathrm{O}\) と紛らわしいから,「ゼロ点」と片仮名で書くようにする。 また基円上の 2 つのゼロ点はいずれも直線 \(\mathrm{M}\) の投影されたものであり,同じものだから区別しない。
大円群が縦の線となるように (ゼロ点が上下にくるように) ステレオネットを置いてみると, 赤道投影ネットには横向きの線も多く描かれていることがわかる。 これらが小円群である。
大円群も小円群も, 図 2.1.1. では \(5^\circ\) 刻みに描かれている。 実習で配布するウルフの赤道投影ネットでは \(1^\circ\) 刻みである。 角度刻みは,ステレオネットによって異なるが,そのこと自体には特に意味はない。 基円が小さくなると \(1^\circ\) 刻みでは線の間隔が狭く煩雑になるので \(2^\circ\) 刻みやそれ以上になっているものもある。 赤道投影ネットであれば,描かれている大円・小円の関係はどれも変わらないし,使い方も同じである。
赤道投影ネットでは,大円群の場合, 投影面と平行な直線 \(\mathrm{M}\) を軸として面を一定の角度刻みに傾けていったときの大円が \(180^\circ\) 分 (半球分) すべて投影されて描かれている。 また \(0^\circ\) と \(180^\circ\) は同じことで,その大円が基円である。 なお通常の赤道投影ネットでは,大円群はその両端 (ゼロ点に近い場所) では一部あるいは全部省略されることが多い ( 図 2.1.1. )。 これは,その辺りでは線が密になりすぎてわかりにくくなるためである。
小円群の方は,球の中心 \(\mathrm{O}\) を通る直線 \(\mathrm{L}\) を直線 \(\mathrm{M}\) から同じく一定の角度刻みに傾けて, それを直線 \(\mathrm{M}\) を軸として回転させたときの小円が \(180^\circ\) 分投影されて描かれている ( 図 2.1.4. )。 ただし \(0^\circ\) と \(180^\circ\) の小円は基円上の点である。 このとき直線 \(\mathrm{L}\) と直線 \(\mathrm{M}\) は同じだから,\(0^\circ\) と \(180^\circ\) の小円 (点) は, 基円上の直線 \(\mathrm{M}\) の投影点 (ゼロ点) に投影される (この点は小円群の \(0^\circ\) の小円だから 「ゼロ点」と呼ぶことにした)。 また \(90^\circ\) のときは大円になる。
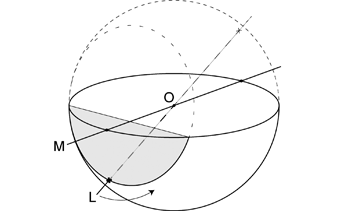
水平面を投影面として地質学的に説明するなら,大円群は走向が等しく傾斜の異なる平面の大円の集まりである。 また小円群は大円群の平面の走向をトレンドとし水平から傾いた (プランジした) 直線 \(\mathrm{L}\) を, 大円群の平面の走向線を軸に回転させた (つまり回転軸は水平) 小円または大円の集まりである。 なお直線は球面と 2 つの交点をもち,それらは互いに球の中心に関して対称だから, ゼロ点が上下になるようにステレオネットを置いたとき, 小円群の上半分は,回転する直線 \(\mathrm{L}\) と球面との交点のうち一方が下半球を通った軌跡, 下半分は先ほどの交点と球の中心に関して対称な交点が下半球を通った軌跡である。 水平な線 (プランジが \(0^\circ\)) の小円は基円上の点 (ゼロ点) である。 またプランジが \(90^\circ\) のときは大円となる。
赤道投影ネットの大円群の大円は,基円に近い側から基円の中心へと,投影面からの傾斜が大きくなる。 基円は投影面と平行な大円 (傾き \(0^\circ\)) であり, 中心を通っている大円 (直線状の大円) は投影面と垂直な面の大円 (傾き \(90^\circ\)) である。 小円群の小円もまた,基円の中心に近いものほど,投影面からより大きく傾いた線の回転の軌跡になっている。 傾き \(0^\circ\) のときの小円はゼロ点である。 また傾き \(90^\circ\) のときは大円であり,小円群で唯一の大円 (直線状の大円) がそれである。
このように,赤道投影ネットの大円群・小円群の大円・小円はいずれも,基円の中心へと,投影面とのなす角が高角なものになる。 このことは忘れないようにしたい。 地質学では面の傾斜・線のプランジを水平面となす角で考える。 したがって水平面を投影面とすれば,面や線と投影面とがなす角とはすなわち面の傾斜・線のプランジである。
これらの大円・小円のうち,中心を通る直線状の大円 (仮想球体の中心を通り投影面に垂直な面の大円) が大円群に 1 つ,小円群にも 1 つあるが,これらは基本的に同じものである。 そのため,角度の関係を見る際には同じように使うことができる。
赤道投影ネットは回転する分度器で考えるとわかりやすい。 \(1^\circ\) 刻みに角度目盛のついた半円状の分度器 (つまり一般的な分度器) を見てみよう。 この分度器を両端の \(0^\circ\) と \(180^\circ\) の目盛 (分度器によって目盛の数字は異なるかもしれない) を結ぶ直線 (これを直線 \(\mathrm{QR}\) と呼ぶことにする) を軸に回転させてみよう。 すると分度器の半円弧の縁 (角度目盛がついている部分,これを弧 \(\mathrm{QR}\) と呼ぼう) が描く軌跡は球になる ( 図 2.1.5. )。
分度器は平面で,しかもこの場合球の中心を通る平面だから,弧 \(\mathrm{QR}\) がすなわち大円群の大円である。 半円状の分度器だから弧 \(\mathrm{QR}\) も大円の半分であるが, 半球投影する場合には投影面と平行な面を除いてすべて大円は半分だけが投影されるわけだから, 分度器で見た大円 (弧 \(\mathrm{QR}\)) こそが投影される大円だと考えれば良い。 \(1^\circ\) 刻みの赤道投影ネットであれば,分度器を \(1^\circ\) ごと回転させていったときの弧 \(\mathrm{QR}\) が 大円群として投影されているわけである。 なおこのとき直線 \(\mathrm{QR}\) が上で説明に使った直線 \(\mathrm{M}\) になっている。
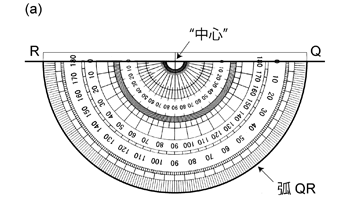
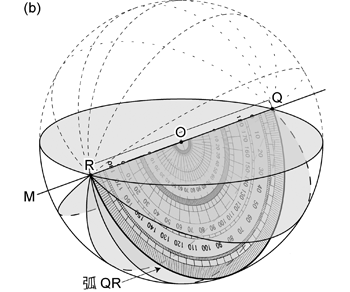
では分度器を回転させた際に,弧 \(\mathrm{QR}\) 上にある角度目盛はどのような軌跡を描くだろうか。 それらの軌跡は回転させた軸 (直線 \(\mathrm{QR}\)) に直交する小円となっているはずである。 このことがよくわからなければ,製図用のコンパス (円を描くために使用されるコンパス) で試してみると良い。 コンパスを適当な角度開いて,片方の足を軸に回転させてみる。 それを軸にしている足の先端側から見れば,もう一方の足の先が円を描いている。 このとき 2 本の足の交点から円を描いている足の先までの距離は一定だから,この円は回転軸に直交している ( 図 2.1.6. a )。
分度器の角度目盛も,回転軸 (直線 \(\mathrm{QR}\)) に対してある角度で斜交した直線であると考えて良いので, これらの軌跡もコンパスの足と同様に回転軸と直交した円を描く。 角度目盛のある弧 \(\mathrm{QR}\) の軌跡が球であることを考えれば,\(90^\circ\) の角度目盛を除いて, 他の角度目盛の軌跡である円はすべて小円であることがわかる ( 図 2.1.6. b )。 \(90^\circ\) の角度目盛の軌跡だけは球の中心を通る円になるので大円である。 \(1^\circ\) 刻みの赤道投影ネットには, 回転する分度器のすべての角度目盛 (目盛が \(1^\circ\) 刻みならば) が描く小円・大円が,小円群として投影されている。
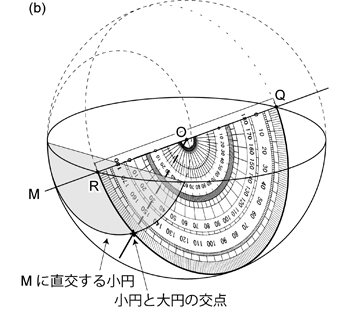
したがって赤道投影ネットでは,大円群の大円はすべて分度器だと考えれば良い。 分度器 (大円群の大円) の角度目盛に相当するのが小円群の小円・大円と大円群の大円との交点である。
ところで角度目盛の軌跡である小円・大円は分度器の回転軸 (直線 \(\mathrm{QR}\)) に直交している。 つまり回転軸を法線とする。 またある回転軸で回転する平面の回転角は,その回転軸を法線とするような平面上で定義される。 例えば地層の走向・傾斜の場合,走向線がこの場合の回転軸に相当し,傾斜は走向線と直交する方向, すなわち走向線を法線とするような面上で測定される。 線のプランジは線を含む鉛直面上で測定されるが,このときその鉛直面は,線の回転軸を法線とする面となっている。 だから,小円群の平面上において,大円群の各大円の傾斜角を測定することができる。
言い換えれば,小円群の小円・大円と大円群の大円との交点を角度目盛と考えれば, 小円群の小円・大円もまた分度器として考えて良い,ということである。 大円群はすべて同じ大きさの分度器で構成されるが,小円群の場合は大きさが異なる。 そして小円群の分度器は,直線 \(\mathrm{M}\) に直交し,かつ分度器の "中心" が常に直線 \(\mathrm{M}\) 上にある。
要するに,赤道投影ネットの大円・小円は,どれも分度器として使うことができるということである。 だから赤道投影ネットを特殊なグラフ用紙のように利用して,線や面を投影したり,簡単な方位解析をおこなうことができるのである。
なお,小円群が大円群の回転軸を法線とすることは,大円群の面と小円群の面は互いに直交していることを意味している。 したがって赤道投影ネットの大円群の大円と小円群の小円・大円は互いに直交している。 ウルフネットは等角投影であるから,ウルフの赤道投影ネットでは大円群の大円と小円群の小円・大円は すべてその交点において直交している (その点における接線同士が直交している)。 シュミットネットでは角度は保存されないので,これらの線は必ずしも直交しない。