この投影が等積投影であることを確認しよう。 等角投影のときと同じように横方向と縦方向の距離の変化率を考える。 球の中心 \({\rm O}\) を通り投影面からのプランジ角 \(\alpha\) (\(0 \le \alpha \lt \pi /2\)) の線 \({\rm L}\) が \({\rm AB}\) を軸として回転したときの 球面と線 \({\rm L}\) との交点 \({\rm X}\) の軌跡を円 \({\rm C}\) とすると， 円 \({\rm C}\) が投影された円 \({\rm C'}\) の半径は， 式 (1.3.21) より \(r_{C'} = R \: \sqrt[]{2 (1 - \sin \alpha)}\) となり， 今度は半径がやや拡大されて投影される。 円 \({\rm C}\) の半径 \(r_{\rm C} = R \cos \alpha\) だから，点 \({\rm X}\) における横方向の距離の変化率 \(m_h\) は，

\begin{align} m_h = \frac{\sqrt[]{2 (1 - \sin \alpha)}}{\cos \alpha} \tag{1.3.25} \end{align}

である。 やはりこれは円 \({\rm C}\) の円周上どの点であっても一定である。 では縦方向の距離の変化率 \(m_v\) はどうか。 こちらも等角投影のときと同じように考えれば良い。 球面と平面 \({\rm ABX}\) の交円上にプランジ \(\alpha + \beta\) の線と仮想球体表面との交点 \({\rm Y}\) を考えるなら， \(BX'\)，\(BY'\) は 式 (1.3.21) で与えられるから，\(g (\alpha) = \: \sqrt[]{2 (1 - \sin \alpha)}\) とおけば，

\begin{align} m_{\beta} = \frac{|g (\alpha) - g (\alpha + \beta)|}{|\beta|} = \frac{g (\alpha) - g (\alpha + \beta)}{\beta} \tag{1.3.26} \end{align}

となり，やはり \(m_v\) は \(\beta \to 0\) のときの \(m_{\beta}\) であるから，

\begin{align} m_v & = \lim_{\beta \to 0} m_{\beta} \nonumber \\ & = - g' (\alpha) \nonumber \\ & = \frac{2 \cos \alpha}{2 \: \sqrt[]{2 (1 - \sin \alpha)}} \nonumber \\ & = \frac{\cos \alpha}{\sqrt[]{2(1 - \sin \alpha)}} \tag{1.3.27} \end{align}

である。 したがって，\(0 \le \alpha \lt \pi /2\) であれば \(m_{h}m_{v} = 1\) だから，点 \({\rm X}\) にある形が投影される際， 横方向に引き伸ばされた分だけ縦方向に縮められることで，面積は変化しないことがわかる。 また \(\alpha = \pi /2\) では，等角投影のときと同じく，縦方向に直交する方向も縦方向であるから， どの方向にも \(m_v = 0\) すなわちそのままの形・面積で投影される。 したがってこの投影法は，球面上の任意の点 \({\rm X}\) にある形が，それが十分小さければ， 投影の際に変形はするものの，面積はそのままに保存されるという等積投影であることがわかる。 例えばトレンド \(t\)，プランジ \(\alpha\) の線 (球体の中心を通る) を軸とする 半頂角 \(\gamma\) の円錐 (頂点を球体の中心とする) と球体との交円は， \(\gamma\) が十分小さければ，\(t\)，\(\alpha\) によらず面積の等しい楕円として投影されるのである。

等積投影では投影時に変形するから小円・大円は円として投影されない。 それどころか 1.3.3. や 1.3.5. の最後の例で言う \(\gamma\) が十分小さくなければ，小円は楕円としてすら投影されない。 このことは円錐の軸のプランジ \(\alpha = 0\) のときを考えればわかる。

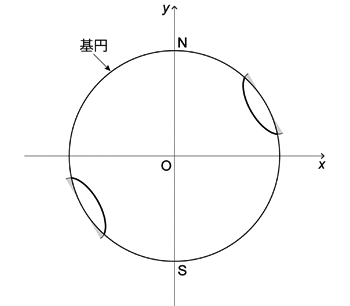
まず，球面上の小円が楕円として投影されるとするなら，小円で囲まれた球面の面積の半分は， 投影された楕円の面積の半分，すなわち半楕円の面積に等しいはずである。 等積投影では面積が保存されるからである。 \(\alpha = 0\) のとき，小円は上半球と下半球で対称だから，もし小円が楕円として投影されるなら， 楕円の長軸と短軸の交点は基円上になければならない。 またそのとき投影されるのは小円の半分であるから，投影面上の小円は，球面上の小円 (半円) と同面積の半楕円となるはずである。 そして上半球側の小円を，基円の中心に関して対称な位置に投影すれば，投影面上には 2 つの大きさの等しい半楕円が投影され， それらの面積の和が，小円で囲まれた球面の面積と等しくなる。 しかし基円は円だから，長軸と短軸の交点が基円上にある以上，投影された楕円は完全な半楕円にはならない。 半楕円の一部が欠けてしまうのである ( 図 1.3.17. )。 そうなると，面積は小円の半分よりも小さくなる。 それでは面積が保存されないことになってしまう。 したがって，面積が保存される以上，小円は必ずしも楕円曲線として投影され得ないのである。 同様に，大円も楕円曲線として投影されない。

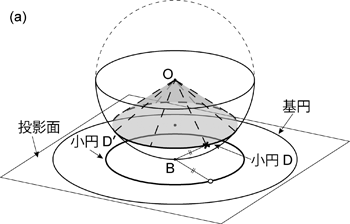
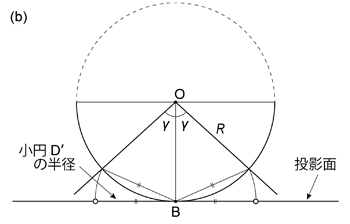
一方で，投影された小円で囲まれた面積は \(t\)，\(\alpha\) によらず常に等しい。 半球表面上で同じ面積であれば，投影されても同じ面積になるはずだからである。 この場合，球面上での面積は，円錐の半頂角 \(\gamma\) にのみ関係することはわかるだろう。 \(\alpha = \pi /2\) のとき，半頂角 \(\gamma\) の円錐と球体との交円 (小円 \({\rm D}\)) は，円として投影される ( 図 1.3.18. )。 投影された小円 \({\rm D'}\) の面積 \(S_{\rm D'}\) は

\begin{align} S_{\rm D'} & = 4 \pi R^2 \sin^2 \left( \frac{\gamma}{2} \right) \\ \nonumber & = 2\pi R^2 (1 - \cos \gamma) \tag{1.3.28} \end{align}

である。 したがって，等積投影では \(t\)，\(\alpha\) によらず，半頂角 \(\gamma\) の円錐と球面との交円は， この式で与えられる面積 \(S_{\rm D'}\) をもつ小円 \({\rm D'}\) (円とも楕円とも限らない) として投影されるのである。

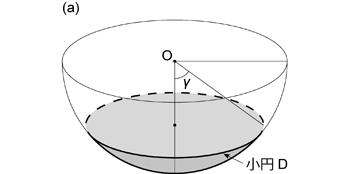
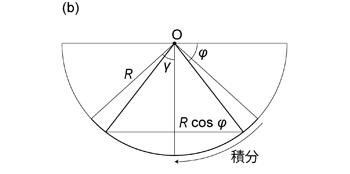
この小円 \({\rm D'}\) の面積は小円 \({\rm D}\) で囲まれた球冠の表面積 \(S_{\rm D}\) に等しい。 等積投影では半球表面で小円に囲まれた範囲にある，あらゆる点における微小な面積は，投影されても保存されるからである。 この球冠の表面積は，円錐の軸を法線とする小円の円周を， 球面に沿って (円錐の軸を含む平面と球との交円の円周に沿って) 積分することで求められるだろう ( 図 1.3.19. )。 小円を描く線のプランジを \(\phi\) とすれば球面上の距離は \(R\phi\) であり， そのときの小円の半径は \(R \cos \phi\) であるから，

\begin{align} S_{\rm D} & = \int_{\frac{\pi}{2} - \gamma}^{\frac{\pi}{2}} 2 \pi R \cos \phi Rd\phi \nonumber \\ & = 2\pi R^2 (1 - \sin (\frac{\pi}{2} - \gamma)) \nonumber \\ & = 2\pi R^2 (1 - \cos \gamma) \tag{1.3.29} \end{align}

式 (1.3.28) と比較すれば \(S_{\rm D} = S_{\rm D'}\) すなわち球面上の面積が， 投影されても保存されていることがわかる。 また，基円の半径 \(r = \: \sqrt[]{2} R\) であるから， この投影では基円の面積は半球の表面積 \(2 \pi R^2\) に等しいが， これは半球表面すべての点における微小な面積が保存されるからである。