この投影では，距離の変化率が \(\alpha\) によって変化するから，面積は保存されない。 また球面上の大きな形は，その微小領域における形は保存されるけれども，全体的には保存されない。 しかし大きくても必ず保存される形がある。 円である。

上で，プランジ \(\alpha\) の線を軸とする半頂角 \(\gamma\) の円錐と球体との交円は， \(\gamma\) が十分小さければそのまま円として投影されると述べたが，等角投影では実は， このような交円は \(\gamma\) の大きさによらず円として投影される。 この交円は言い換えれば，中心を通らない面と球面との交円であるから，小円である。 つまり等角投影では小円は投影面上でも円として投影されるということである。

トレンド \(t = 0\) (北向き)，プランジ \(\alpha\) \((0 \le \alpha \le \pi /2)\) の線 \({\rm L_1}\) を回転軸とし， それと \(\gamma\) \((0 \lt \gamma \le \pi /2)\) だけ斜交する線 \({\rm L_2}\) を回転させたときの， \({\rm L_2}\) と球体表面との交円を小円 \({\rm D}\) として，三次元の直交座標系で考える ( 図 1.3.12. )。 小円 \({\rm D}\) はすなわち \({\rm L_1}\) を軸とする半頂角 \(\gamma\) の円錐と球体表面との交円である。 仮想球体の中心 \({\rm O}\) を原点とし，南北方向を \(y\) 軸 (北向きが正)， 水平面上でそれと直交する方向に \(x\) 軸 (東向きが正)，鉛直方向に \(z\) 軸 (上向きが正) をとる。 このとき仮想球体の半径を \(R\) とすると，球面上の点 \((x,~y,~z)\) には，

\begin{align} x^2 + y^2 + z^2 = R^2 \tag{1.3.13} \end{align}

が成り立つ。

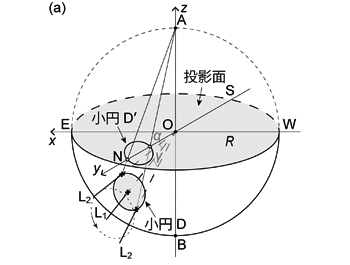
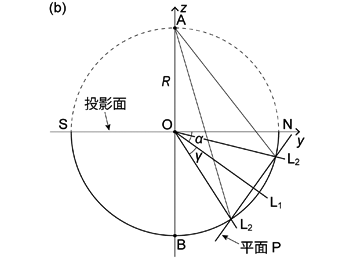
また小円 \({\rm D}\) は円錐の軸 \({\rm L_1}\) を法線とする平面 \({\rm P}\) と球体表面との交円だと考えることもできる。 したがって小円 \({\rm D}\) は平面 \({\rm P}\) 上にある。 \({\rm L_1}\) は \(x\) 軸に直交し，プランジ \(\alpha\) だから， 平面 \({\rm P}\) の法線ベクトルは \((0,~\cos \alpha,~-\sin \alpha)^{\rm T}\) ということになる。 またこの平面 \({\rm P}\) は，平面 \({\rm P}\) と \({\rm L_1}\) との交点 \((0,~R\cos \gamma \cos \alpha,~-R\cos \gamma \sin \alpha)\) を通る。 したがって平面 \({\rm P}\) 上の点 \((x,~y,~z)\) には，

\begin{align} & \cos \alpha (y - R\cos \gamma \cos \alpha) - \sin \alpha (z + R\cos \gamma \sin \alpha) \\ \nonumber = &~ y \cos \alpha - z \sin \alpha - R \cos \gamma = 0 \tag{1.3.14} \end{align}

が成り立つ (平面の方程式に関しては実習の手引きを参照)。 小円 \({\rm D}\) は球と平面との交円だから，当然小円 \({\rm D}\) 上の点には 式 (1.3.13) と (1.3.14) が同時に成り立つ。

小円 \({\rm D}\) 上の点 \({\rm X_1}\) の座標を \((x_1,~y_1,~z_1)\)， 投影面上 (\(z = 0\)) で \({\rm X_1}\) の投影された点 \({\rm X_1'}\) の座標を \((x_1',~y_1',~0)\) とすると， 式 (1.3.2)， (1.3.3)， (1.3.13)， (1.3.14) を使って，

\begin{align} & x_1'^2 + \left( y_1' - \frac{R \cos \alpha}{\sin \alpha + \cos \gamma} \right)^2 = \frac{R^2 \sin^2 \gamma}{(\sin \alpha + \cos \gamma)^2} \nonumber \\ \tag{1.3.15} \end{align}

という，\(x_1'\)，\(y_1'\) の関係を表す式が得られる (途中経過は実習の手引きを参照)。 この式は言うまでもなく，\((x_1',~y_1')\) が投影面上において， 中心 \((0,~R \cos \alpha / (\sin \alpha + \cos \gamma),~0)\)， 半径 \(R \sin \gamma / (\sin \alpha + \cos \gamma)\) の円上にあることを示している。 したがって，小円 \({\rm D}\) が投影された小円 \({\rm D'}\) は円である。

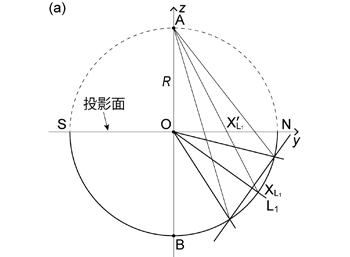
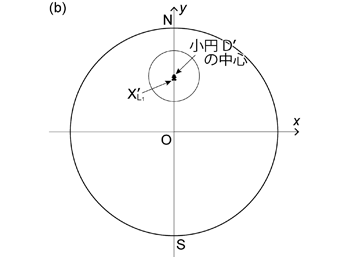
ここで注意したいのは小円 \({\rm D'}\) の中心が 円錐の軸 \({\rm L_1}\) と球面との交点 \({\rm X_{L_1}}\) の投影点 \({\rm X_{L_1}'}\) ではないことである ( 図 1.3.13. )。 \({\rm L_1}\) はトレンド \(0\)，プランジ \(\alpha\) の線だから， \({\rm X_{L_1}'}\) は \(y\) 軸上にあり，その \(y\) 座標は 式 (1.3.1)， (1.3.3) より，

\begin{align} y_{\, \rm X_{L_1}'} = \frac{R \cos \alpha}{1 + \sin \alpha} \tag{1.3.16} \end{align}

ということになる。 小円 \({\rm D'}\) の中心の \(y\) 座標 \(R \cos \alpha / (\sin \alpha + \cos \gamma)\) と比べると， \(\cos \gamma \lt 1\) だから，小円 \({\rm D'}\) の中心の \(y\) 座標の方が， \({\rm X_{L_1}'}\) の \(y\) 座標よりもやや大きい。 つまり小円 \({\rm D'}\) の中心は，\({\rm X_{L_1}'}\) よりもやや基円よりに位置する (図 1.3.13. b )。

ここまではトレンド \(t = 0\) としてきたが，\(t \neq 0\) の場合も，\(y\) 軸を \(t\) と平行にとれば，全く同じことになる。 したがって，等角投影では任意の小円は円として投影される。

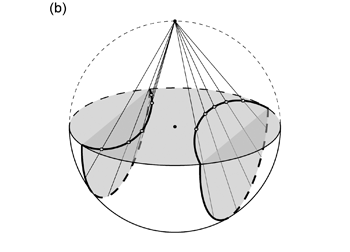
なお，このとき \(\alpha\) と \(\gamma\) の関係によっては，円錐は下半球だけでなく上半球とも交わることがある。 つまり小円 \({\rm D}\) が下半球だけに収まらず，上半球にはみ出す。 そのような場合，小円 \({\rm D}\) は円の一部である円弧として投影される。 また，円錐側面を，球の中心 \({\rm O}\) を通る直線の集合と考えれば (円錐の軸と交角 \(\gamma\) で斜交する線を， 円錐の軸を回転軸として回転させた軌跡だと考えれば)，小円 \({\rm D}\) の上半球にある部分は， それと球の中心に関して対称な位置で下半球にあることになる ( 図 1.3.14. a )。 線と球面との 2 つの交点のうち，片方が上半球にあるならば， もう一方は上半球にある交点と球の中心に関して対称な位置で下半球にあるからである。 投影面上では，基円の中心を挟んだ反対側に，残りの小円が円弧として投影されることになる ( 図 1.3.14. b )。 このときの線の回転と小円との関係は，ステレオネットを使った回転操作をおこなう際に利用するから，覚えておいてほしい。

等角投影では大円もまた円弧として投影されることについても見ておこう。 先に考えた面 \({\rm P}\) (南北走向，傾斜角 \(\theta\) で東傾斜) をもう一度例にとる。 \(\theta = 0\) ならば基円として投影されるから，円であることはすでにわかっている。 また他の姿勢の面についても \(x\) 軸，\(y\) 軸を適当にとれば，下の説明と同じように考えることができるから， どのような姿勢の面であれ大円は円弧として投影されることになる。

\(0 \lt \theta \lt \pi /2\) のとき，面 \({\rm P}\) はトレンド \(t\) \((0 \le t \le \pi /2)\)， プランジ \(\alpha\) でトレンドとプランジに 式 (1.3.4) の関係があるような線の集合として投影されるのであった。 投影面上に東西方向を \(x\) 軸，南北方向を \(y\) 軸とする直交座標 (それぞれ東向き，北向きが正) をとれば， 大円上の点が投影される位置は 式 (1.3.1)， (1.3.2)， (1.3.3) で与えられる。

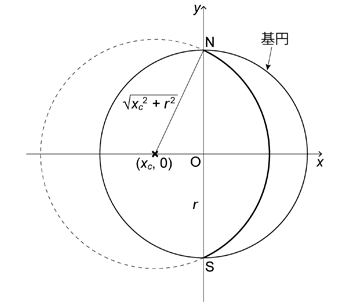
面 \({\rm P}\) は南北走向だから， 面 \({\rm P}\) と球面との交線である大円は \(xz\) 平面 (東西走向の鉛直面) に関して対称であり， そのため投影面上に投影される大円は \(x\) 軸に関して対称でなければならない。 ということは，投影される大円が円弧であるならばその中心は \(x\) 軸上にあるはずである。 そこでその座標を \((x_c,~0)\) とする。 また基円の半径を \(r\) としたとき，投影された大円は必ず \((0,~r)\) を通るから， 円弧の半径は \(\sqrt{x_c^2 + r^2}\) であろう ( 図 1.3.15. )。 そして，

\begin{align} (x - x_c)^2 + y^2 & = x_c^2 + r^2 \\ \nonumber x^2 + y^2 - 2x_cx & = r^2 \tag{1.3.17} \end{align}

が \(t\)，\(\alpha\) に関わらず成り立たなければならない。 式 (1.3.2)， (1.3.3) より，

\begin{align} & OX'^2 \sin^2 t + OX'^2 \cos^2 t - 2x_c OX' \sin t \\ \nonumber = & OX'^2 - 2x_c OX' \sin t = r^2 \tag{1.3.18} \end{align}

であり， 式 (1.3.1)， (1.3.4) を利用すれば，

\begin{align} \frac{r^2 \cos^2 \alpha}{(1 + \sin \alpha)^2} - \frac{2x_cr \cos \alpha \tan \alpha}{(1 + \sin \alpha) \tan \theta} & = r^2 \\ \nonumber x_c & = - r \tan \theta。 \tag{1.3.19} \end{align}

つまり，投影された大円は \(t\)，\(\alpha\) に関わらず，\((- r \tan \theta,~0)\) を中心とし， 半径 \(r \: \sqrt{1 + \tan^2 \theta}\) の円弧になっているのである。 \(\theta = \pi /2\) の場合だけは，大円は円弧ではなく線分として投影されるが， これは半径無限大の円弧と考えれば，すべての大円は円弧で投影されると言えよう。