球面投影
1. 球面投影の原理
1.3. 等角投影・等積投影
1.3.2. 等角性の確認
以下では再び投影面を，中心を通る平面として解説する。 当然，投影面を仮想球体上の 1 点における球体の接平面とした場合も同じことが言えるので，気になる人は自分で確かめてみてほしい。
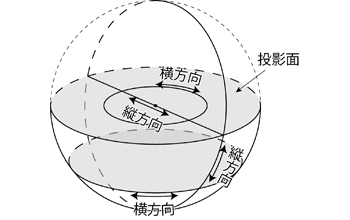
ではここまで解説してきた投影法が等角投影であることを確認してみよう。 上で述べたように，等角投影では球体表面の任意の点にある形が (十分小さければ)，そのままの形で投影される。 ここでは下半球投影を例にとって考えてみる。 投影面と平行な面で球を切ると，その断面は円になる (切った面が投影面でなければ小円・投影面であれば大円)。 そこでこの円の円周方向を横方向と呼ぶことにする ( 図 1.3.8. )。 また球面上でこの横方向と直交する向きを縦方向と呼ぼう ( 図 1.3.8. )。 縦方向は投影面と垂直な大円の円周方向である。 また縦方向は投影されると，基円の中心を通る直線状の大円の方向になる。
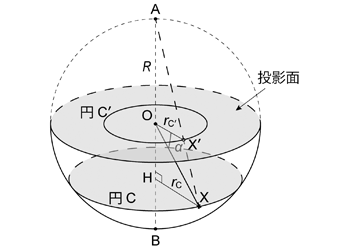
さて球の中心 \({\rm O}\) を通り投影面 (今は水平面) からのプランジ \(\alpha\) の線 \({\rm L}\) が \({\rm AB}\) を軸として回転したとき，球面と線 \({\rm L}\) との交点 \({\rm X}\) の軌跡は， \(0 \le \alpha \lt \pi /2\) であれば，半径 \(r_{\rm C} = R \cos \alpha\) の円 \({\rm C}\) になる。 この円は投影面上にも円 \({\rm C}'\) (\({\rm X}\) が投影された \({\rm X}'\) の軌跡) として投影されるが， 投影法からわかるように投影面上の円 \({\rm C}'\) の半径 \(r_{\rm C'}\) は \(r_{\rm C}\) よりも小さい ( 図 1.3.9. )。 したがって円 \({\rm C}\) の円周上の距離，つまり横方向の距離は，縮小されて投影されることになる。 このとき点 \({\rm X}\) に関する横方向の距離の変化率 \(m_h\) は，円 \({\rm C}\) の円周上のどの点においても一定で， 円 \({\rm C}\) の円周に対する円 \({\rm C}'\) の円周の比に等しく，また当然ながら円周の比は半径の比に等しい。 そこで \({\rm X}\) から直線 \({\rm AB}\) に垂線を引き，その足を \({\rm H}\) とすると ( 図 1.3.9. )，\(OX' : HX = AO : AH\) であるから，
\begin{align} m_h & = \frac{R}{R (1 + \sin \alpha)} \\ \nonumber & = \frac{1}{1 + \sin \alpha} \tag{1.3.7} \end{align}
となる。 つまり球面上で点 \({\rm X}\) に何かの形があった場合， その形は投影される際，横方向に \(1 / (1 + \sin \alpha)\) 倍に縮小されるということである。
では次に点 \({\rm X}\) に関する縦方向の距離の変化率 \(m_v\) を考えてみよう。 この場合，横方向の距離の変化率 \(m_h\) のときのように， 球面上での大円の円周に対する投影された大円の長さの比から \(m_v\) を求めることはできない。 なぜなら \({\rm X}\) の投影点である \({\rm X}'\) と基円の中心との距離 \(OX'\) は， 式 (1.3.1) より， \(\alpha\) の余角 (正確には余角の半角) の正接関数に比例する， つまり \(\alpha\) によって \(OX'\) 自体の変化率が一定ではないからである。 そのため，横方向の距離の場合は円 \({\rm C}\) の円周上どの点であっても投影された際の距離の変化率 \(m_h\) は一定だったが， 縦方向では \({\rm X}\) が球面上で大円の円周のどこにあるか (すなわち \(\alpha\) の大きさ) によって投影された際の距離の変化率 \(m_v\) は変化する。
\(\alpha\) と \(OX'\) の直交座標系で考えてみよう。 そのとき 式 (1.3.1) は曲線になる ( 図 1.3.10. )。 この曲線の任意の \(\alpha\) における接線の傾きは，その \(\alpha\) のときの \(OX'\) の変化率である。 そして点 \({\rm X}\) に関する \(m_v\) とはつまり \(OX'\) の変化率の大きさだから，\(\alpha\) における接線の傾きの絶対値である。 したがって，\(m_v = | f' (\alpha) |\) であり，\(f'(\alpha)\) は \(0 \le \alpha \lt \pi /2\) で一貫して負だから，
\begin{align} m_v = | f' (\alpha) | & = - f' (\alpha) \\ \nonumber & = \frac{\sin \alpha (1 + \sin \alpha) + \cos^2 \alpha}{(1 + \sin \alpha)^2} \\ \nonumber & = \frac{1 + \sin \alpha}{(1 + \sin \alpha)^2} \\ \nonumber & = \frac{1}{1 + \sin \alpha} \tag{1.3.8} \end{align}
となる。
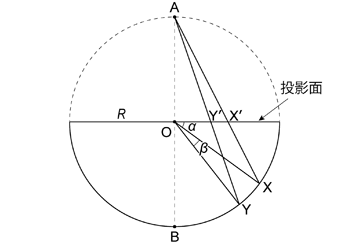
よくわからなければ次のように考えれば良い。 球面と平面 \({\rm ABX}\) との交円上にプランジ \(\alpha + \beta\) \((\beta \neq 0)\) の線と 仮想球体表面との交点 \({\rm Y}\) があったとき，弧 \(XY = |R\beta|\) である。 この距離は， \({\rm Y}\) の投影された点を \({\rm Y}'\) とすれば， 距離 \(X'Y'\) に縮小されて投影される ( 図 1.3.11. )。 \(OX'\)，\(OY'\) は 式 (1.3.1) で求められ，\(f (\alpha) = \cos \alpha / (1 + \sin \alpha)\) とおけば，
\begin{align} X'Y' & = |OX' - OY'| \\ \nonumber & = |R f (\alpha) - R f (\alpha + \beta)| \tag{1.3.9} \end{align}
である。したがって弧 \({\rm XY}\) が投影された際の距離の変化率 \(m_{\beta}\) は，
\begin{align} m_{\beta} & = \frac{|R\left( f (\alpha) - f (\alpha + \beta) \right)|}{|R\beta|} \\ \nonumber & = \frac{|f (\alpha) - f (\alpha + \beta)|}{|\beta|} \tag{1.3.10} \end{align}
ということになる。
式 (1.3.10) の分子を見れば， 絶対値の中は \(\beta \gt 0\) のとき正 (\(OX' \gt OY'\)となるから) である。 そのとき分母の絶対値の中は当然正である。 また \(\beta \lt 0\) だと，分子側は負 (\(OX' \lt OY'\)) であり，分母側もまた負である。 そのため 式 (1.3.10) は，\(\beta\) の正負に関わらず，
\begin{align} m_{\beta} = \frac{ f (\alpha) - f (\alpha + \beta)}{\beta} \tag{1.3.11} \end{align}
である。
\(m_v\) とは点 \({\rm X}\) に関する縦方向の距離の変化率だから，\(\beta \to 0\) のときの \(m_{\beta}\) である。 したがって，
\begin{align} m_v & = \lim_{\beta \to 0} m_{\beta} \nonumber \\ & = \lim_{\beta \to 0} \frac{f (\alpha) - f (\alpha + \beta)}{\beta} \end{align}
となるが，これはほとんど導関数の定義式であるから，
\begin{align} m_v = \lim_{\beta \to 0} m_{\beta} & = - f' (\alpha) \\ \nonumber & = \frac{1}{1 + \sin \alpha} \tag{1.3.12} \end{align}
ということである。
これは当然ながら 式 (1.3.8) と変わらない。 式 (1.3.7) と比較して， \(0 \le \alpha \lt \pi /2\) では任意の点 \({\rm X}\) に関して \(m_h = m_v\) であることがわかる。 横方向と縦方向の縮小率が等しければ形は変わらない。
\(\alpha = \pi /2\) のときは，横方向を定義できないが，縦方向と直交する方向も縦方向になるから，どの方向にも \(m_v = 1/2\) で縮小されると言える。 したがってこの投影法では任意の点 \({\rm X}\) に関して横方向と縦方向の縮小率が等しく，球体表面にある形は，それが十分小さければ，投影の際に縮小されはするものの，形はそのままに保存されるといえる。 例えばトレンド \(t\)，プランジ \(\alpha\) の線 (球体の中心を通る) を軸とする半頂角 \(\gamma\) の円錐 (頂点を球体の中心とする) と球体との交円は，\(\gamma\) が十分小さければ，\(t\)，\(\alpha\) によらず，そのまま円として投影される。 また形が変化しないということは，その形を構成するあらゆる角度がそのままに投影される，つまり角度が保存されるということことである。 これで等角投影であることが確認できた。