固体地球内部の物質の性質とその変化 〜密度を例にして〜 (第9.1章、第10.3章、第9.4章)
地球の内部は、我々が住んでいる地球の表面 (1気圧、常温) と比べて高い圧力や温度がかかっている。 このような条件のもとでは、物質の「固さ」や「重さ」といった性質や特徴が大きく異なってくることが期待される。 ここではその一例として、地球内部にある物体の密度とそれが変化する仕組みについて考える。
第5回では、物体にはたらく2種類の力として「面積力」と「体積力」があることを述べた。 そのうち「体積力」の代表的なものは物体にはたらく重力であるが、重力の大きさはその物体の密度 (単位体積あたりの質量) によって決まる。 また第6回で物体の変形を学んだ際に、応力を受けたことによって生じる物体の変形には体積の変化を伴うもの (体積ひずみ \(\Theta\)) もあることも見てきた。 すなわち、地球内部にある物体の密度 (あるいは体積) がどのように変化するかを知ることは、地球内部における力のかかり具合や運動のようすを推測するための第一歩といえる。
以下この授業では簡単のため、モノの種類や組成 (+量) は変化しない場合に話を限定し、「温度や圧力が変わると物質の密度がどう変わるか?」を考えてみる。 これは物質の「状態方程式」(理想気体でいうところの \(pV=nRT\)) に関係してくる。 また以下で、圧力や温度を変えたことによる密度 (あるいは体積) の変化を調べていくのだが、これは高校の物理で「理想気体の状態変化」の際に出てきた「○○変化」のうちの3つに対応している。 (当然ながら、体積の変わらない「定積変化」はここには出てこない)
| 圧力を変える | 温度を変える | |
|---|---|---|
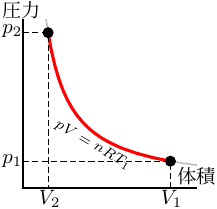
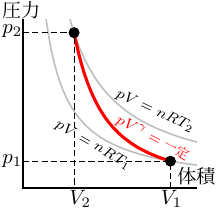
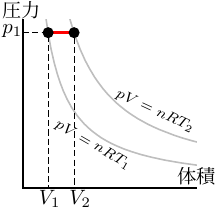
| 等温変化 | 断熱変化 | 定圧変化 |
 |
 |
 |
圧力による密度変化 (第9.1.1章)
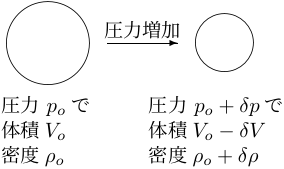一般に、圧力が高くなると物体はちぢむ。
この現象を「圧縮 (compression)」という。
圧縮されると、物体の体積が減り、密度が増える。
物体が圧力を受けて縮む度合は「体積弾性率 (bulk modulus)」または「非圧縮率」という量で測られる。 体積弾性率 (非圧縮率) \(K\) は以下のように定義される。 \begin{equation} \begin{split} \frac{1}{K}& \equiv\frac{体積の減少率}{圧力の増加量} =\frac{\delta{V}/V_o}{\delta{p}} \\& \equiv\frac{密度の増加率}{圧力の増加量} =\frac{\delta{\rho}/\rho_o}{\delta{p}} \end{split} \tag{9.4'} \end{equation} 分子の項が変化「量」ではなく変化「率」になっているのに注意。 例えば体積は、考える物体の分量 (モル数とか質量とか) によって変わってしまう (熱力学で出てくる用語では「示量性状態量」という) ものであるから、体積の変化「量」そのものを考えても意味がないからである。
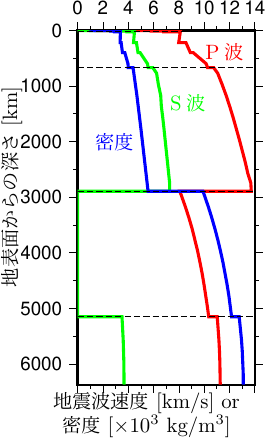
体積弾性率 \(K\) は圧力と同じく [Pa] の単位をもち、マントルを構成する岩石ではおよそ数百 GPa (\(10^{11}\) Pa) 程度の値をもつ。 地球内部で予想される圧力 (マントル内で最大 135 GPa) によって構成物質は大きく圧縮され、その密度は有意に変化する。 地球内部の密度の変化の図 (PREM; 図9.2や図10.3) によるとマントルの上下で約65%の密度の増加があるが、その大部分は圧縮によるもの。
ここで定義した体積弾性率 \(K\) は、第6回で出てきた Lamé 定数 (\(\lambda\) および \(\mu\)) との間に \(K=\lambda+(2/3)\mu\) という関係がある。
圧縮による密度変化は熱対流にさほど影響しない。 「同じ深さでも密度が違う」と浮力が生じるのだが、圧縮による密度変化それ自身が浮力を生むのではないのが理由。
また、第7回で登場した地震波速度の式から単純に想像すると、地下深くになって密度 \(\rho\) が増えると地震波速度は遅く (\(\propto\sqrt{1/\rho}\)) なるように思えてしまいそうなものだが、PREM の図からも分かるように、実際の地球内部ではそうなっていない。その理由は、深くなれば物質の密度も大きくなるが、その物質の弾性定数がもっと大きくなってしまう (要するに「硬さ」がものすごく増す) から。
温度による密度変化 (10.3.1章)
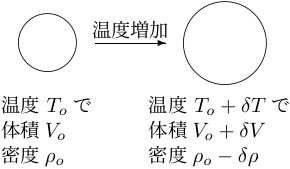一般に、温度が高くなると物体はふくらむ (図10.13)。
この現象を「熱膨張 (thermal expansion)」という。
熱膨張すると、物体の体積が増え、密度が減る。
物体が熱膨張する度合は「熱膨張率 (coefficient of thermal expansion)」と いう量で測られる。 熱膨張率 \(\alpha_v\) は以下のように定義される。 \begin{equation} \begin{split} {\alpha_v}& \equiv\frac{体積の増加率}{温度の増加量} =\frac{{\delta{V}}/V_o}{{\delta{T}}} \\& \equiv\frac{密度の減少率}{温度の増加量} =\frac{\delta{\rho}/\rho_o}{{\delta{T}}} \end{split} \tag{10.3} \end{equation} ここでも分子の項が変化「量」ではなく変化「率」になっているのに注意。 ただしより正確には微分 (もっと正確にいえば「偏微分」)を用いて \begin{equation} {\alpha_v}\equiv\frac{1}{V}\left(\frac{\partial{V}}{\partial{T}}\right)_{p} =-\frac{1}{\rho}\left(\frac{\partial{\rho}}{\partial{T}}\right)_{p} \tag{10.4} \end{equation} と与えられる。 上式で下付き添字の \(p\) は、圧力 \(p\) を一定に保った状態で偏微分することを示し ている。
熱膨張率は [K-1] の単位をもち、地球内部を構成する物質ではおおよそ \({\alpha_v}\approx10^{-5}\) K-1 程度の値である。 数百 K の温度差で密度がやっと 1% 変化するような小さいものであるが、熱対流はこのわずかな密度の差で起こっている。
相転移による密度変化 (第10.3.1章、第9.4章)
「相 (phase)」とは、物質のもつ構造の状態のこと。 例えば物質の三態 (気体・液体・固体) など。
「相転移 (phase transition)」とは、温度や圧力などの変化によって、ある相から別の相へ変化すること。 分かりやすい「相転移」として、物質の三態の変化を伴うもの。 例えば
- 氷 ↔ 水 ↔ 水蒸気の変化
- 状態は固体 ↔ 液体 ↔ 気体と変わっている。
- 化学組成は H2O で変わらない。
- ドライアイス ↔ 炭酸ガス(二酸化炭素) の変化
- 状態は固体 ↔ 気体と変わっている。(昇華)
- 化学組成は CO2 で変わらない。
- 固体の岩石と液体のマグマ
- 外核 (液体金属) と内核 (固体)
| グラファイト | ダイヤモンド | |
|---|---|---|
| 色 | 黒 | 透明 |
| 硬度 | 1-2 | 10 |
| 電気 | 通す | 通さない |
| 比重 | 2.28 | 3.52 |
- グラファイト (黒鉛 or 石墨) とダイヤモンド
- 三態 (固体) も化学組成 (C; 炭素) も変わらないが、
- 炭素原子のつながり具合が変わっている。
- マントルの主要構成鉱物の1つであるカンラン石 (Mg,Fe)2SiO4 の一連の相転移 (第9.4章)
- 深くなるほど圧力が大きくなることによって相転移を起こし、結晶構造 (構成する原子と原子のつながり具合) が変わる。
- さらに最近は、太陽系外の巨大地球型惑星「スーパー地球」のマントルの中で起こりそうな鉱物の相転移までもが調べられるようになっている。
「多形」の話では、実は水 (氷) も面白い例。ふだん目にする氷は「Ih相」(六方晶系; 水晶とか方解石と同じ) というものだが、過冷却の状態では「Ic相」(立方晶系; 岩塩とかダイヤモンドと同じ) という構造になるし、また圧力の高い状態になればさらに異なる結晶構造をとる。氷の多形については最近でも盛んに研究が行われており、2021年には20種類めにあたる「XIX相」が新しく発見された。
マントルを構成する鉱物の相転移は、地球内部構造と重要な関係がある。 相転移が起これば、その深さで鉱物の性質が急激に変化する。 PREM の図に見える密度や地震波速度の不連続な変化には、相転移が関係しているものもある。