固体地球物理学概論 (2024年前学期) 第05回

連続体力学入門: 地球内部での運動を記述する物理法則 (第10.3.1章)

運動方程式
質量	\(\times\)	加速度	\(=\)	力
\(m\)	\(\times\)	\(a\)	\(=\)	\(f\)

地学コース/地球科学科の2年後期の授業「海洋物理学I」(森本先生) でも習うはずの「ナビエ・ストークス方程式」が、地球内部の運動を記述する時にも登場する。 式の見た目はとても難しいのだが、そのココロはあの「ニュートンの運動の法則」 (慣性の法則、運動方程式、作用・反作用の法則) である。 そのため、地球内部にある 物体にはどんな力がはたらいているか? を知ることからスタートする。

ちょっとその前に余談: 物理学で扱う「物体」の運動の分類

質点の運動	剛体の運動	連続体の運動

物体の運動を学ぶ物理学は、だいたい以下のような体系からできている。 当然ながら、下のものほど難しくなる。

1. 「質点の運動」: イメージでいうと「太陽のまわりを公転している地球」
   • 並進運動 (高校の物理だと \(m\times{a}=f\) と習ったもの) を対象にする。
   • 物体の「位置」が時間とともに変化する様子を調べる。
   • 物体の「運動のしにくさ」は「質量」で表わされる。
2. 「剛体の運動」: イメージでいうと「自転しながら公転している地球」
   • 「質点の運動」に加えて、回転運動も対象にする。
   • 物体の「位置」に加えて「向き」が時間とともに変化する様子を調べる。
   • 物体の「運動のしにくさ」は「質量」と「慣性モーメント」で表わされる。
3. 「連続体 (固体・流体) の運動」: イメージでいうと「地殻活動しながら自転・公転している地球」
   • 「剛体の運動」に加えて、物体内部の変形も対象にする
   • 物体の「位置」と「向き」に加えて「形」が時間とともに変化する様子を調べる。

体積力と面積力

力を2種類に区別する。

体積力 (body force):

物体の体積や質量に比例してはたらく力。 重力、電磁気力、慣性力 (コリオリ力) など

面積力 (surface force):

物体を囲んでいる面の大きさに比例してはたらく力。 圧力、応力など

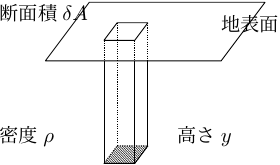右図のように、地面の中に置かれた角柱を例に考えると(図10.11)、

• 角柱にはたらく重力は \(\rho{g}{y}{\delta{A}}\) [N]
• 角柱の底の面にはたらく圧力は \(\dfrac{\rho{g}{y}{\delta{A}}}{{\delta{A}}}=\rho{g}{y}\) [N/m²]

これらの力の合計 (合力) をとって、運動を調べることになる。

弾性や粘性による力は、面積力に分類される。 そのため、(地球内部を含む) 連続体の運動に対しては、面積力が重要になってくる。

面積力とは

• 面に対する向きの違う2種類の面積力

  面に対する力の向きの違いによって、2種類の面積力がありえる。(右図; 図10.14a)
  • 面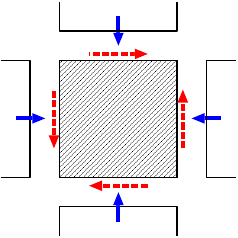を 垂直に押す 力 (面に 直角に はたらく)
    「圧力」 (または法線応力)
  • 面を 横にずらす 力 (面に 平行に はたらく)
    「せん断応力」 (または接線応力)
  
  

• 自分と周囲との面積力の及ぼしあい

  接触面を通して互いに力を及ぼしあっている。(右図; 図10.14b)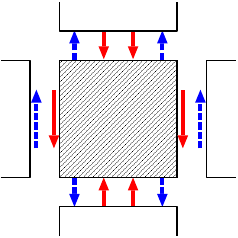
  • 作用・反作用の法則により、

    (自分が周囲から受ける力) = −(自分が周囲に及ぼす力)

    マイナスがついているのは、「向きが反対」という意味。 しかも「マイナス1倍」だから、向きは反対でも大きさは同じ。
  
  
• 面積力を指定するには、2つの方向を指定してやる必要がある
  1. どの 方向 にはたらく面積力? (力 の方向)
  2. どの 面 にはたらく面積力? (面の法線の方向)

応力を指定するのに登場する2つの添字

一般に、2つの方向 (ベクトル) を指定することによって定まる量は「2階のテンソル」と呼ばれ、連続体の変形を議論する場面でよく登場する。 応力も2階のテンソルであるから、

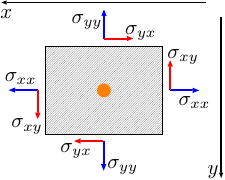• 応力を正確に表現するには、\(\sigma_{xx}\)、\(\sigma_{xy}\)、\(\sigma_{xz}\) のように、2つの添字がつけられる。 それぞれの添字で、面の法線の方向と力の方向を表す。
  • 2つの添字が同じものは、面を垂直に押す 力
  • 2つの添字が異なるものは、面を横にずらす 力
• 3次元の物体にかかる応力は \(3\times3=9\) 個の「成分」で表現される。 (2次元だったら \(2\times2=4\) 個)

ただし、応力の「成分」のうち、2つの添字が異なるものについては

• 物体の中心 (図の●の点) のまわりでの、力のモーメントのつりあいを考えると、\(\sigma_{xy}=\sigma_{yx}\) という関係が成り立つ。 同様に \(\sigma_{xz}=\sigma_{zx}\) および \(\sigma_{yz}=\sigma_{yx}\) も成り立つ。

なお、このような性質をもつ量は「対称テンソル」と呼ばれる。

弾性による面積力

• 面を垂直に押す力	面を横にずらす力

  弾性による面積力のうち
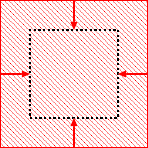
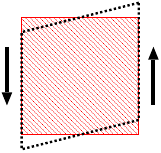
  • 面を 垂直に押す 力が P波 に関係する
  • 面を 横にずらす 力が S波 に関係する
• 流体では面を 横にずらす 弾性ははたらかない (だからS波が伝わらない)。
• 弾性による力の大きさは、「ひずみ (歪; strain)」が大きいと大きい。

「ひずみ」とは、物体の変形のパターンや大きさに関する量で、物体の位置の変化をいう「変位 (displacement)」の空間変化率にあたる。 ひずみも2階のテンソルである。 ひずみの定義は次回に触れるが、教科書では地殻変動を議論している第3.1章にも説明がある。

粘性による面積力

• 粘性による面積力の大きな特徴は、面を垂直に押す方向だけでなく、面を 横にずらす 方向にも力がはたらくこと。
• 粘性による力は、流体を周囲となるべく同じ速さで動かそうとする傾向にはたらく。

  粘性のある流体の動きの例として、コップの中の水をマドラーでかき回すような状況をイメージしてみるのもよいだろう。 かき回すとコップの中の水全体が回り始めるが、ここでのポイントは マドラーが押していないところの水まで動かされている こと。 その反対に、かき回すのをやめると、だんだんと動きが弱まり、最後には止まってしまう。

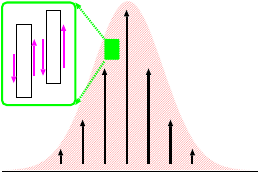• 地球内部で粘性のある流れの例として、下面境界から発生する上昇流について考えると (右図; 図10.15)
  1. 流体のある部分が持ち上がろうとする
  2. 粘性によってその周辺部も引きずられて持ち上げられる
  3. さらにその周辺部も引きずられて持ち上げられる
  この繰り返しにより、水平方向に広がった上昇流の塊ができる。 「ねばねば」した流体ほど、この塊は水平方向に大きくなる。
• 固体地球科学の守備範囲の中で、粘性が出てくる他の例の1つは、溶岩とかマグマ。 溶岩やマグマの粘性が違うと、火山の形や噴火の様式も違ってくる。 このあたりのくわしい話は教科書第4章を。
• 粘性による力の大きさは、「ひずみ速度 (strain rate)」が大きいと大きい。
  「ひずみ速度」とは、物体の変形のパターンや速さに関する量で、物体の流れの速さの空間変化率にあたる。 ひずみ速度も2階のテンソルである。