固体地球物理学概論 (2024年前学期) 第6回

連続体力学入門(その2) 物体の変形 (第3.1章)

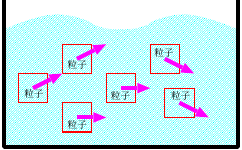
大気や海洋の流れを考える際と同様に、固体地球内部の運動や変形を考える際には「流体力学」 (あるいはさらに一般化した「連続体力学」) という物理学の分野の原理が用いられる。 そこでは、固体や流体の運動・変形を考える手段として、物体を仮想的な「粒子」(つぶ) の集まりだとみなす。 そしてこれらの仮想的な「粒子」の運動や、「粒子」どうしの力のつりあいを考える。 例えばコップの中に入っている水の運動を調べたいときには、多数の流体「粒子」がコップの中をすき間なく埋めており、ある流体「粒子」のまわりには別の多数の流体「粒子」が必ずあるものと仮定している。 このような仮定のもとで、1つ1つの流体「粒子」の運動のようすを考えていく。

第5回 では流体の中に置かれた「物体」にはたらく力を考えてきたが、実はそれは 個々の流体「粒子」がどんな力を受けているか? を考えていたことに相当する。 今回は、流体「粒子」の変形を記述する方法を考えてみる。

変位とひずみ

「変位 (displacement)」とは、物体の内部の点の位置の変化をあらわすベクトル。 右下図で、破線が変形する前のかたち、実線が変形した後のかたち、矢印が4つの頂点の変位を表わしているとする。

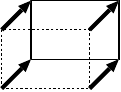• もし変位が一様 (場所によらず同じ方向に同じ大きさだけ変位) であれば、物体は変形したことにならない。(右図; 図3.1a も参照)
  
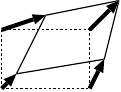• もし変位が一様でない (場所によって変位の方向や大きさが異なっている) と、物体は変形したことになる。 (右図; 図3.1b も参照)
  

「ひずみ (strain)」とは、変位の空間的な変化率 (変位を空間の座標で微分したもの)。 ここでは、ひずみが大きくない場合の理論 (「無限小ひずみ」の理論) に則って話を進める。

ひずみの定義

ひずみも2階のテンソルであるので

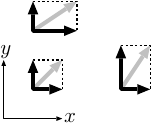
• 「変位の方向」と「変位の変化する方向」の2つの方向 (ベクトル) を指定する必要がある。
  右図の例で、ある点ともう1つの点との間で変位の違いを調べようとする場合でいうと、
  • 「変位の方向」とは、それぞれの点における矢印の方向のこと。
  • 「変位の変化する方向」とは、変位を比較するそれら2点を結ぶ線の方向のこと。
• 応力と同じように、ひずみも2つの添字をつけて表示される。 そのため、\(e_{xx}\)、\(e_{xy}\)、\(e_{xz}\) など9つの成分があるが、次に示すように独立な成分は6つ。
• 2つの方向の関係の違いによって、2種類のひずみがありえる。
  • 伸びひずみ (「変位の方向」と「変位の変化する方向」が同じ)
    2つの添字が同じものが伸びひずみ (\(e_{xx}\)、\(e_{yy}\)、\(e_{zz}\) の3つ)
  • 剪断ひずみ (「変位の方向」と「変位の変化する方向」が異なる)
    2つの添字が異なるものが剪断ひずみ (それ以外の6つ; 本当は3つ)

伸びひずみ

変形前	変形後

もともと \(dx\) だった線分PQの長さが変形後に \((1+e_{xx})\) 倍になったとする (右図; 図3.2b)。 変形後の長さについて \(dx+du=dx(1+e_{xx})\) が成り立つから、\(e_{xx}=\dfrac{du}{dx}\)。 これより、\(x\) 方向の伸びひずみを、偏微分を用いて \begin{equation} e_{xx}\equiv\frac{\partial{u}}{\partial{x}} \tag{3.1} \end{equation} と書く。 \(e_{yy}\) や \(e_{zz}\) も同様。 この定義から分かるように、ひずみには単位がない (無次元量という)。 \[ \frac{\text{点Pと点Qの変位の違い [m]}}{\text{点Pと点Qの間の距離 [m]}} =\text{単位なし} \]

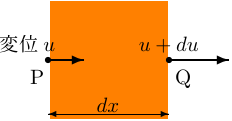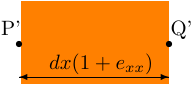また、変形後の物体の体積を調べてみると、 \begin{align*} {dx}(1+e_{xx})\times{dy}(1+e_{yy})\times{dz}(1+e_{zz})& ={dx}{dy}{dz}(1+e_{xx})(1+e_{yy})(1+e_{zz}) \\& ={dx}{dy}{dz}\left[1+\left(e_{xx}+e_{yy}+e_{zz}\right)+\left(e_{xx}e_{yy}+e_{yy}e_{zz}+e_{zz}e_{xx}\right)+e_{xx}e_{yy}e_{zz}\right] \end{align*} であるが、変形がごく小さい (\(e_{xx}\)、\(e_{yy}\)、\(e_{zz}\) が 0 に近い) と仮定すれば、この式は \[ {dx}(1+e_{xx})\times{dy}(1+e_{yy})\times{dz}(1+e_{zz}) \simeq{dx}{dy}{dz}(1+e_{xx}+e_{yy}+e_{zz}) \] と近似してよい。 ここで \begin{equation} \Theta\equiv{e_{xx}+e_{yy}+e_{zz}} \tag{3.5'} \end{equation} と書くと、これは変形後に物体の体積が \((1+\Theta)\) 倍になったことを意味する。 この \(\Theta\) を体積ひずみという。 (ただし教科書では2次元の話なので「面積ひずみ」となっている)

剪断ひずみ

変形前	変形後

もともと直角だった ∠QPR が、変形によってどれだけ変わったかを調べる (右図; 図3.2d)。

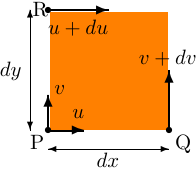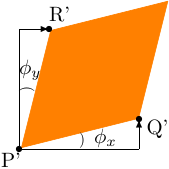• 線分PQの角度変化量 \(\phi_x\)は (反時計回りを正として) \(\phi_x\simeq\tan\phi_x=\dfrac{d{v}}{d{x}}\)
• 線分PRの角度変化量 \(\phi_y\) は (時計回りを正として) \(\phi_y\simeq\tan\phi_y=\dfrac{d{u}}{d{y}}\)

ここでも、変形がごく小さい (\(\phi_x\) も \(\phi_y\) も 0 に近い) という仮定により、\(\tan\phi_x\simeq\phi_x\) かつ \(\tan\phi_y\simeq\phi_y\) と近似できることを利用している (ただし角度の単位はラジアン)。 これより、 \begin{equation} e_{xy}=e_{yx}=\frac{\phi_x+\phi_y}{2} =\frac{1}{2}\left(\frac{\partial{v}}{\partial{x}}+\frac{\partial{u}}{\partial{y}}\right) \tag{3.2} \end{equation} と書く。 \(e_{xz}=e_{zx}\) や \(e_{yz}=e_{zy}\) も同様に成り立つ。 これより、剪断ひずみの成分6つのうち、独立なものはその半分の3つだけである。

なお、剪断ひずみを式(3.2)のような「2つの角度の平均」として定義する理由は、角度が変わる際に物体全体が回転する効果を取り除きたいからである。実際 \(\phi_x\not=\phi_y\) の場合には、物体には変形だけでなく回転も起こったことになる。[パラパラまんが風の説明]

この定義より、2つの添字の順番が入れかわっても、ひずみの大きさは同じである。 これと同じ「対称性」は、第5回で登場した応力にも備わっていたことを思い出そう。 すなわち、応力もひずみも2階の対称テンソルであるということになる。

弾性体の応力とひずみの関係

ここでも話を簡単にするため、等方弾性体 (弾性の性質が方向によらない) につ いてのみ考える。 また一般的に、 \begin{equation} \sigma_{xy}=\sigma_{yx} ,\quad \sigma_{yz}=\sigma_{zy} ,\quad \sigma_{xz}=\sigma_{zx} \end{equation} という関係 (「応力テンソルの対称性」) も成り立つので、応力テンソルの成分9個のうち、6個のみを考えればよい。

等方弾性体では、応力 \(\sigma\) とひずみの間には、次のような関係がある (Hooke の法則に対応)。 \begin{equation} \begin{split} \sigma_{xx}&=\lambda\Theta+2\mu{e_{xx}} =(\lambda+2\mu){e}_{xx}+\lambda{e}_{yy}+\lambda{e}_{zz}\\ \sigma_{yy}&=\lambda\Theta+2\mu{e_{yy}} =\lambda{e}_{xx}+(\lambda+2\mu){e}_{yy}+\lambda{e}_{zz}\\ \sigma_{zz}&=\lambda\Theta+2\mu{e_{zz}} =\lambda{e}_{xx}+\lambda{e}_{yy}+(\lambda+2\mu){e}_{zz}\\ \sigma_{xy}&=2\mu{e_{xy}}\\ \sigma_{yz}&=2\mu{e_{yz}}\\ \sigma_{xz}&=2\mu{e_{xz}}\\ \end{split} \end{equation} ここで、\(\lambda\) と \(\mu\) は物質の弾性的な性質を表わす量で、「ラメ定数 (Lamé's constants)」とよばれる。 2つのラメ定数のうち、特に \(\mu\) は「剛性率 (rigidity)」ともよばれる。 これら2つのラメ定数と密度 \(\rho\) によって、地震波のP波やS波の伝わる速度が表わされる。

2つあるラメ定数のうち、法線成分 (2つの添字が同じもの) の関係式にだけ登場している \(\lambda\) は、他の場面で使われているのをあまり見たことがない。 その理由の1つは、体積ひずみと法線応力との関係を忠実に表わすには、\(\lambda\) だと不十分だからではないかと (亀山は) 思う。 実際、等方弾性体の応力 \(\sigma\) とひずみ \(e\) の関係のうち、法線成分の関係を表わす3つの式で辺々和をとってみると、 \(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}=3\lambda\Theta+2\mu\left({e_{xx}}+{e_{yy}}+{e_{zz}}\right)=(3\lambda+2\mu)\Theta\) であるが、これをさらに変形すると \[ \frac{\sigma_{xx}+\sigma_{yy}+\sigma_{zz}}{3}=\left(\lambda+\frac{2}{3}\mu\right)\Theta \] と書ける。 この式の左辺が圧力 (=まわりから均等にかかってくる法線応力) であることに注意すると、圧力と体積ひずみ \(\Theta\) の間を結んでいるのは \(\lambda\) ではなく \(\lambda+\frac{2}{3}\mu\) であることが分かる。 この \(\lambda+\frac{2}{3}\mu\) は「体積弾性率 (bulk modulus)」などと呼ばれており、物質の「状態方程式」を考えるときなどにも登場する (例えば第9.1.1章など)。