マントル対流数値シミュレーション概論 1 マントル対流を記述する方程式の導出 A マントル対流に必要な熱力学

2 マントル対流の解析的研究

(February 9, 2022)

2.1 対流の起こり始めに関する線型安定性解析

ここでは線型安定性解析と呼ばれる理論に基づいて、熱対流の起こり始める条件について検討する。以下の手順は、 [1, 8, 6, 10] などに倣った。

簡単のため、ブシネスク近似が成り立ち、かつ物性が一様な流体の、水平方向に無限の広がりをもつ3次元領域の中での熱対流を仮定する。無次元化された基礎方程式を具体的に書き下すと、

$\displaystyle 0$	$\displaystyle=-\frac{\displaystyle\partial p}{\displaystyle\partial x_{i}}+% \frac{\displaystyle\partial^{2}v_{i}}{\displaystyle\partial x_{j}^{2}}+Ra\,T% \delta_{iz}$	(2.1)
$\displaystyle 0$	$\displaystyle=\frac{\displaystyle\partial v_{k}}{\displaystyle\partial x_{k}}$	(2.2)
$\displaystyle\frac{\displaystyle\partial T}{\displaystyle\partial t}$	$\displaystyle=-v_{j}\frac{\displaystyle\partial T}{\displaystyle\partial x_{j}% }+\frac{\displaystyle\partial^{2}T}{\displaystyle\partial x_{\ell}^{2}}$	(2.3)

ただし温度場 $T$ の境界条件として

T=0\text{~{}at~{}}z=1,\quad T=1\text{~{}at~{}}z=0

鉛直方向速度 $v_{z}$ の境界条件として

v_{z}=0\text{~{}at~{}}z=0,1

を考える。また水平方向速度 $v_{x}$ 及び $v_{y}$ の境界条件は

	自由すべり境界	$\displaystyle\frac{\displaystyle\partial v_{x}}{\displaystyle\partial z}=\frac% {\displaystyle\partial v_{y}}{\displaystyle\partial z}=0\text{~{}at~{}}z=0,1$		(2.4)
	固着境界	$\displaystyle u_{x}=v_{y}=0\text{~{}at~{}}z=0,1$		(2.5)

のいずれかであるものとする。この種の問題では、Rayleigh 数がある値 $Ra_{c}$ (臨界 Rayleigh 数) より大きければ対流が起こることが示されている。ここでは、線型安定性解析により $Ra_{c}$ を求めてみる。線型安定性解析のよくある手順に倣い、各変数を基本場と微小な擾乱の和で書く。以下、添字 ${}_{o}$ つきで基本場を表わし、 $\prime$ つきで微小な擾乱を表わすことにする。

まず、基本場の表現を決定する。簡単のため、基本場は完全静止( $v_{oi}=0$ )な熱伝導状態で、水平面内( $x$ -及び $y$ -方向)には一様とする。この場合、基本場は以下のように表わせる。

	$\displaystyle 0$	$\displaystyle=\frac{\displaystyle d^{2}T_{o}}{\displaystyle dz^{2}}\quad% \Rightarrow T_{o}=1-z$		(2.6)
	$\displaystyle 0$	$\displaystyle=-\frac{\displaystyle dp_{o}}{\displaystyle dz}+Ra\,T_{o}$		(2.7)

次に、微小な擾乱に関する式を求める。線型安定性解析の定石に倣い、擾乱は微小とみなして1次の項のみ残すと、速度及び圧力の微小な擾乱に関する式は以下のように書ける。

	$\displaystyle 0$	$\displaystyle=-\frac{\displaystyle\partial p\prime}{\displaystyle\partial x_{i% }}+\frac{\displaystyle\partial^{2}v_{i}\prime}{\displaystyle\partial x_{j}^{2}% }+Ra\,T\prime\delta_{iz}$		(2.8)
	$\displaystyle 0$	$\displaystyle=\frac{\displaystyle\partial v_{k}\prime}{\displaystyle\partial x% _{k}}$		(2.9)

これらから $v_{x}\prime$ 、 $v_{y}\prime$ 、 $p\prime$ を消去してやることにより、 $v_{z}\prime$ (以下簡単のため $w\prime$ と略記する) に関する式を得る。

\nabla^{4}{w\prime}+Ra\left(\nabla^{2}-\frac{\displaystyle\partial^{2}}{% \displaystyle\partial z^{2}}\right)T\prime=0

(2.10)

同様に、温度場の微小擾乱に関する式を求めると、

	$\displaystyle\frac{\displaystyle\partial T\prime}{\displaystyle\partial t}$	$\displaystyle=-v_{j}\prime\frac{\displaystyle\partial(T_{o}+T\prime)}{% \displaystyle\partial x_{j}}+\frac{\displaystyle\partial^{2}(T_{o}+T\prime)}{% \displaystyle\partial x_{\ell}^{2}}\simeq-v_{j}\prime\frac{\displaystyle% \partial T_{o}}{\displaystyle\partial x_{j}}+\frac{\displaystyle\partial^{2}T% \prime}{\displaystyle\partial x_{\ell}^{2}}$
		$\displaystyle=w\prime+\nabla^{2}T\prime$		(2.11)

さらに中立 (臨界) 状態を仮定して温度擾乱の時間変化がないとすれば、

\displaystyle 0

\displaystyle=w\prime+\nabla^{2}T\prime

(2.12)

(2.10) と (2.12) から $T\prime$ を消去すれば、 $w\prime$ のみを含んだ方程式

\displaystyle\nabla^{6}{w\prime}=Ra\left(\nabla^{2}-\frac{\displaystyle% \partial^{2}}{\displaystyle\partial z^{2}}\right){w\prime}

(2.13)

を得る。また連続の式を使うことにより水平方向速度場の境界条件を $w\prime$ を含む形で書き直せば

	自由すべり境界	$\displaystyle\frac{\displaystyle\partial^{2}w\prime}{\displaystyle\partial z^{% 2}}=0\text{~{}at~{}}z=0,1$		(2.14)
	固着境界	$\displaystyle\frac{\displaystyle\partial w\prime}{\displaystyle\partial z}=0% \text{~{}at~{}}z=0,1$		(2.15)

を得る。同様に式(2.10)を用いて $T\prime$ の境界条件を $w\prime$ のみで書き表わすと、

\displaystyle\nabla^{4}{w\prime}=0\text{~{}at~{}}z=0,1

(2.16)

となる。

これらは $w\prime$ に関する定数係数の微分方程式であり、変数分離法により解を求めることができる。そこで

{w\prime}\equiv{W(z)}\exp\left[i({k_{x}}x+i{k_{y}}y)\right]

(2.17)

なる形の解を仮定する。ここで $i$ は虚数単位である。これを用いれば、解くべき方程式は結局

	$\displaystyle\left(\frac{\displaystyle d^{2}}{\displaystyle dz^{2}}-K^{2}% \right)^{3}{W}+Ra{K^{2}}{W}=0$		(2.18)
	$\displaystyle\text{自由すべり境界の場合~{}}W=\frac{\displaystyle d^{2}W}{\displaystyle dz% ^{2}}=\left(\frac{\displaystyle d^{2}}{\displaystyle dz^{2}}-K^{2}\right)^{2}{% W}=0\text{~{}at~{}}z=0,1$		(2.19)
	$\displaystyle\text{固着境界の場合~{}}W=\frac{\displaystyle dW}{\displaystyle dz}=% \left(\frac{\displaystyle d^{2}}{\displaystyle dz^{2}}-K^{2}\right)^{2}{W}=0% \text{~{}at~{}}z=0,1$		(2.20)

とまとめられる。ただし $K\equiv\sqrt{{k_{x}}^{2}+{k_{y}}^{2}}$ は水平方向の擾乱の波数である。

2.1.1 上下の境界面がいずれも自由すべり面の場合

この場合が最も簡単に臨界Rayleigh数 $Ra_{c}$ を求めることができる。境界条件(2.19)より、 $W$ は

W(z)=\sum_{n\geq{1}}{U_{n}}\sin(n\pi{z})

(2.21)

と書ける。これを式(2.18)に代入して整理すると、

\displaystyle\sum_{n}{U_{n}}\sin(n\pi{z})\left\{-\left[(n\pi)^{2}+K^{2}\right]% ^{3}+{Ra}{K^{2}}\right\}=0

(2.22)

これが自明 ( $U_{n}=0$ ) でない解を持つためには

-\left[(n\pi)^{2}+K^{2}\right]^{3}+{Ra}{K^{2}}=0\quad\Rightarrow\quad Ra=\frac% {\displaystyle\left[(n\pi)^{2}+K^{2}\right]^{3}}{\displaystyle K^{2}}

(2.23)

と与えられる。

この最小値を求めよう。上式を $K$ で微分して

\displaystyle\frac{\displaystyle dRa}{\displaystyle dK}=\frac{\displaystyle 2% \left[(n\pi)^{2}+K^{2}\right]^{2}}{\displaystyle K^{3}}[2K^{2}-(n\pi)^{2}]

(2.24)

これは

K=\frac{\displaystyle n\pi}{\displaystyle\sqrt{2}}

(2.25)

のとき $0$ となり、その時の $R a$ は

Ra=\frac{\displaystyle\left[(n\pi)^{2}+\frac{\displaystyle(n\pi)^{2}}{% \displaystyle 2}\right]^{3}}{\displaystyle\frac{\displaystyle(n\pi)^{2}}{% \displaystyle 2}}=\frac{\displaystyle 27}{\displaystyle 4}(n\pi)^{4}

(2.26)

である。これから、 $n=1$ のときに臨界Rayleigh数 $Ra_{c}$ は最小値

Ra_{c}=\frac{\displaystyle 27}{\displaystyle 4}\pi^{4}\simeq{657.51}

(2.27)

をとり、これを与える擾乱の水平方向波数 $K$ は

K=\frac{\displaystyle\pi}{\displaystyle\sqrt{2}}

(2.28)

である。

2.1.2 上下の境界面がいずれも固着面の場合

この場合には、境界条件から $W(z)$ の関数形を直ちに推測することが困難である。そこで、解をより一般的な表現で書き表わした後に、境界条件を満足するようにとることにする。

$W(z)$ は $\exp(\pm{q}z)$ (ただし $q$ は複素数) の線形結合 (即ち、 $\sin(qz)$ 、 $\cos(qz)$ 、 $\sinh(qz)$ 、 $\cosh(qz)$ の線型結合) で書けるはずである。この関数形を式(2.18)に代入すると、自明でない解が存在するためには $q$ は

(q^{2}-K^{2})^{3}+Ra{K^{2}}=0

(2.29)

を満足しなければならない。これを解くため $Ra=\tau^{3}K^{2}$ と置くと、

q^{2}=-K^{2}\left({\tau}\sqrt[3]{1}-1\right)

(2.30)

である。ただし

\sqrt[3]{1}=e^{0},\exp\left(i\frac{\displaystyle 2\pi}{\displaystyle 3}\right)% ,\exp\left({i\frac{\displaystyle 4\pi}{\displaystyle 3}}\right)=1,\frac{% \displaystyle-1\pm\sqrt{3}{i}}{\displaystyle 2}

は1の3乗根である。この6つの解を $\pm{i}{q_{0}}$ 、 $\pm{q}$ 、 $\pm{q^{\ast}}$ ( ${}^{\ast}$ は複素共役) とおくと、

$\displaystyle q_{0}$	$\displaystyle=K\sqrt{\tau-1}$	(2.31)
$\displaystyle q_{1}\equiv\Re(q)$	$\displaystyle=\frac{\displaystyle K}{\displaystyle 2}\left[\sqrt{1+\tau+\tau^{% 2}}+\left(1+\frac{\displaystyle\tau}{\displaystyle 2}\right)\right]$	(2.32)
$\displaystyle q_{2}\equiv\Im(q)$	$\displaystyle=\frac{\displaystyle K}{\displaystyle 2}\left[\sqrt{1+\tau+\tau^{% 2}}-\left(1+\frac{\displaystyle\tau}{\displaystyle 2}\right)\right]$	(2.33)

と書ける。またこれらの間には

(q_{0}^{2}+K^{2})^{2}=K^{4}\tau^{2},\quad(q^{2}-K^{2})^{2}=\frac{\displaystyle 1% }{\displaystyle 2}K^{4}\tau^{2}\left(-1\pm\sqrt[3]{1}\right)

(2.34)

なる関係がある。

以下、境界条件の対称性より、対流層の真ん中の深さを $z=0$ 、かつ境界面の位置を $z=\pm 1/2$ ととり直す。また $z=0$ に関する対称性から、 $W(z)$ は偶関数となるか奇関数となるかのいずれかである。しかし奇関数の解は $z=0$ で節をもつ( $W(z=0)=0$ )ので、いわゆる「基底状態」ではない。対流の起こり始めとしては、節のない偶関数の解が適当である。そこで、 $W(z)$ が偶関数となるような解を求めてみる。このとき $W(z)$ は

W(z)={a_{0}}\cos({q_{0}}z)+{a_{1}}\cosh({q}z)+{a_{1}^{\ast}}\cosh({q^{\ast}}z)

(2.35)

と書けるはずである。これが境界条件を満たすように係数 ${a_{0}}$ 、 ${a_{1}}$ 、 ${a_{1}^{\ast}}$ を定める。 $W(z)$ を微分すると、

$\displaystyle\frac{\displaystyle dW}{\displaystyle dz}$	$\displaystyle=-{a_{0}}{q_{0}}\sin({q_{0}}z)+{a_{1}}{q}\sinh({q}z)+{a_{1}^{\ast% }}{q^{\ast}}\sinh({q^{\ast}}z)$	(2.36)
$\displaystyle\left(\frac{\displaystyle d^{2}}{\displaystyle dz^{2}}-K^{2}% \right)^{2}{W}$	$\displaystyle={a_{0}}({q_{0}}^{2}+K^{2})^{2}\cos({q_{0}}z)+{a_{1}}(q^{2}-K^{2}% )^{2}\cosh({q}z)+{a_{1}^{\ast}}({q^{\ast}}^{2}-K^{2})^{2}\cosh({q^{\ast}}z)$
	$\displaystyle=K^{4}\tau^{2}\left[{a_{0}}\cos({q_{0}}z)+\frac{\displaystyle% \sqrt{3}i-1}{\displaystyle 2}{a_{1}}\cosh({q}z)-\frac{\displaystyle\sqrt{3}i+1% }{\displaystyle 2}{a_{1}^{\ast}}\cosh({q^{\ast}}z)\right]$	(2.37)

$z=\pm{1/2}$ での境界条件は

$\displaystyle 0$	$\displaystyle={a_{0}}\cos\left(\frac{\displaystyle q_{0}}{\displaystyle 2}% \right)+{a_{1}}\cosh\left(\frac{\displaystyle q}{\displaystyle 2}\right)+{a_{1% }^{\ast}}\cosh\left(\frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)$	(2.38)
$\displaystyle 0$	$\displaystyle=-{a_{0}}{q_{0}}\sin\left(\frac{\displaystyle q_{0}}{% \displaystyle 2}\right)+{a_{1}}{q}\sinh\left(\frac{\displaystyle q}{% \displaystyle 2}\right)+{a_{1}^{\ast}}{q^{\ast}}\sinh\left(\frac{\displaystyle q% ^{\ast}}{\displaystyle 2}\right)$	(2.39)
$\displaystyle 0$	$\displaystyle={a_{0}}\cos\left(\frac{\displaystyle q_{0}}{\displaystyle 2}% \right)+\frac{\displaystyle\sqrt{3}i-1}{\displaystyle 2}{a_{1}}\cosh\left(% \frac{\displaystyle q}{\displaystyle 2}\right)-\frac{\displaystyle\sqrt{3}i+1}% {\displaystyle 2}{a_{1}^{\ast}}\cosh\left(\frac{\displaystyle q^{\ast}}{% \displaystyle 2}\right)$	(2.40)

これを整理すると

\left[\begin{array}[]{ccc}\cos\left(\frac{\displaystyle q_{0}}{\displaystyle 2% }\right)&\cosh\left(\frac{\displaystyle q}{\displaystyle 2}\right)&\cosh\left(% \frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)\\ -{q_{0}}\sin\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)&{q}\sinh% \left(\frac{\displaystyle q}{\displaystyle 2}\right)&{q^{\ast}}\sinh\left(% \frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)\\ 0&\cosh\left(\frac{\displaystyle q}{\displaystyle 2}\right)(\sqrt{3}-i)&\cosh% \left(\frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)(\sqrt{3}+i)\\ \end{array}\right]\left[\begin{array}[]{c}a_{0}\\ a_{1}\\ a_{1}^{\ast}\\ \end{array}\right]=0

(2.41)

これが自明でない解を持つためには、

	$\displaystyle 0$	$\displaystyle=\left\|\begin{array}[]{ccc}\cos\left(\frac{\displaystyle q_{0}}{% \displaystyle 2}\right)&\cosh\left(\frac{\displaystyle q}{\displaystyle 2}% \right)&\cosh\left(\frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)\\ -{q_{0}}\sin\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)&{q}\sinh% \left(\frac{\displaystyle q}{\displaystyle 2}\right)&{q^{\ast}}\sinh\left(% \frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)\\ 0&\cosh\left(\frac{\displaystyle q}{\displaystyle 2}\right)(\sqrt{3}-i)&\cosh% \left(\frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)(\sqrt{3}+i)\\ \end{array}\right\|$
		$\displaystyle=\cos\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)% \cosh\left(\frac{\displaystyle q}{\displaystyle 2}\right)\cosh\left(\frac{% \displaystyle q^{\ast}}{\displaystyle 2}\right)\left\|\begin{array}[]{ccc}1&1&1% \\ -{q_{0}}\tan\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)&{q}\tanh% \left(\frac{\displaystyle q}{\displaystyle 2}\right)&{q^{\ast}}\tanh\left(% \frac{\displaystyle q^{\ast}}{\displaystyle 2}\right)\\ 0&\sqrt{3}-i&\sqrt{3}+i\\ \end{array}\right\|$		(2.42)

これを解いて整理すると、

\displaystyle 0

\displaystyle=-2{q_{0}}\tan\left(\frac{\displaystyle q_{0}}{\displaystyle 2}% \right)+(\sqrt{3}i-1){q}\tanh\left(\frac{\displaystyle q}{\displaystyle 2}% \right)-(\sqrt{3}i+1){q^{\ast}}\tanh\left(\frac{\displaystyle q^{\ast}}{% \displaystyle 2}\right)

(2.43)

あるいは

-{q_{0}}\tan\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)=\frac{% \displaystyle\left({q_{1}}+{q_{2}}\sqrt{3}\right)\sinh\left({q_{1}}\right)+% \left({q_{1}}\sqrt{3}-{q_{2}}\right)\sin\left({q_{2}}\right)}{\displaystyle% \cosh\left({q_{1}}\right)+\cos\left({q_{2}}\right)}

(2.44)

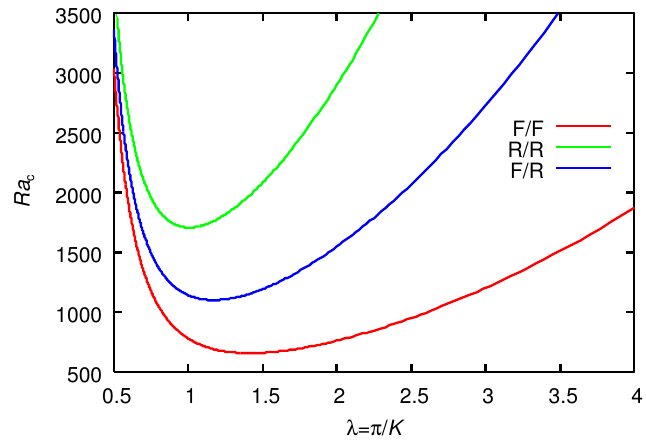
を得る。式 (2.44) によって、 $K$ と $\tau$ ( $=\sqrt[3]{Ra/K^{4}}$ ) が結ばれている。この式の解を数値的に求めると、 $R a$ が最小となるのは $K=3.117$ のときで、このとき $Ra=1707.762$ となる。

なお、 $W(z)$ が奇関数となるときの解を求めてみると、このとき $W(z)$ は

W(z)={a_{0}}\sin\left({q_{0}}z\right)+{a_{1}}\sinh\left({q}z\right)+{a_{1}^{% \ast}}\sinh\left({q^{\ast}}z\right)

(2.45)

とおける。先と同様にしてやると、 ${q_{0}}$ 、 ${q_{1}}$ 、 ${q_{1}^{\ast}}$ に関して、

{q_{0}}\cot\left(\frac{\displaystyle q_{0}}{\displaystyle 2}\right)=\frac{% \displaystyle\left({q_{1}}+{q_{2}}\sqrt{3}\right)\sinh\left({q_{1}}\right)-% \left({q_{1}}\sqrt{3}-{q_{2}}\right)\sin\left({q_{2}}\right)}{\displaystyle% \cosh\left({q_{1}}\right)-\cos\left({q_{2}}\right)}

(2.46)

が成りたつ。 $R a$ が最小となるのは $K=5.365$ のときで、このとき $Ra=17610.39$ となる。

2.1.3 上下の境界面の一方が自由すべり面、もう一方が固着面のとき

このときの解は、両端が剛体面のときの解のうち、奇関数の解から得られる (これは $z=0$ での境界条件を満たしていることに注意)。この解を適用するには、箱の深さが $\frac{\displaystyle 1}{\displaystyle 2}$ になったとみなせばよいので、 $R a$ が最小となるのは $K=5.365/2=2.683$ のときで、このとき $Ra=17610.39/2^{4}=1100.65$ となる。

2.1.4 まとめ

図4に擾乱の水平方向波数 $K$ に対する $Ra_{c}$ の変化を示す。

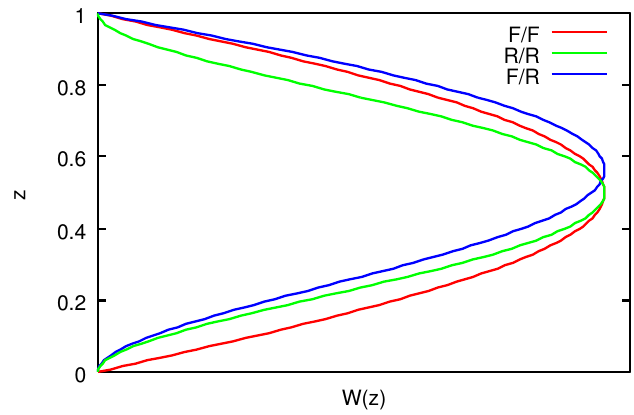
Figure 4: (a) 擾乱の水平方向波数 $K$ に対する $Ra_{c}$ の依存性、(b) $Ra_{c}$ が最小となるときの $W(z)$ の関数形。図中、 “F/F” は上下の境界がいずれも自由すべり面の場合、 “R/R” は上下の境界がいずれも固着面の場合、 “F/R” は一方が自由すべり面でもう一方が固着面の場合を示す。ただし (a) の横軸は $\pi/K$ で与えられる対流セルのアスペクト比でとっている。また (b) のグラフにおいて、 $W(z)$ は最大が1になるように規格化して示している。