マントル対流数値シミュレーション概論マントル対流数値シミュレーション概論 2 マントル対流の解析的研究

1 マントル対流を記述する方程式の導出

まず、3次元デカルト座標系内での流体の運動を記述する一般的な方程式の形を示す。その後、マントル対流の性質を利用して方程式を簡単化する。

なお、この章の記述は [6, 13]を参考にした。

1.1 基礎方程式

流体の運動を記述する基本的な方程式は、質量、運動量、エネルギーの保存則である。これに加え、状態方程式、及び輸送係数(熱伝導率や粘性率)を規定する方程式を含めて、閉じた基礎方程式系を構成する。

1.1.1 質量保存則

\frac{\displaystyle\partial\rho}{\displaystyle\partial t}+\frac{\displaystyle% \partial}{\displaystyle\partial x_{i}}(\rho v_{i})=0

(1.1)

ここで、 $\rho$ は流体の密度、 $\bm{v}=(v_{1},v_{2},v_{3})$ は流体の速度である。

よく知られているLagrange微分 (または実体微分)

\frac{\displaystyle D}{\displaystyle Dt}=\frac{\displaystyle\partial}{% \displaystyle\partial t}+v_{i}\frac{\displaystyle\partial}{\displaystyle% \partial x_{i}}

を使って式(1.1)を書き直すと

\frac{\displaystyle 1}{\displaystyle\rho}\frac{\displaystyle D\rho}{% \displaystyle Dt}+\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{% i}}=0

(1.2)

を得る。この式の左辺第1項は、ある一定の質量を持つ流体素片が占める体積の変化を表している。特に非圧縮( $\rho$ が一定)の場合にはさらに

\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{i}}=0

(1.3)

と簡略化される。

1.1.2 運動量の保存則

\rho\frac{\displaystyle Dv_{i}}{\displaystyle Dt}=-\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}+\frac{\displaystyle\partial\tau_{ij}}{% \displaystyle\partial x_{j}}+\rho g_{i}

(1.4)

この式の左辺は単位体積の流体素片の質量( $\rho$ )と加速度の積、即ち流体素片の持つ運動量の時間変化を表す。

右辺第1項と第2項は流体素片にはたらく表面力(面を通してはたらく力)を表す。このうち、第1項は流体の圧力 $p$ による等方的な応力、第2項は偏差応力テンソル (deviatoric stress tensor) $\tau_{ij}$ で表される非等方的な応力である。流体素片にはたらくトルクのつりあいを考えると、偏差応力テンソルは対称テンソル

\tau_{ij}=\tau_{ji}

(1.5)

であることがわかる。

右辺第3項は流体素片にはたらく体積力を表す。ここでは体積力は重力のみを考え、その他の力(電磁気的な力やコリオリ力など) は考えない。後に示すように、マントル対流のような遅い流れでは、コリオリ力の影響は無視できる。

1.1.3 構成方程式とNavier-Stokes方程式

物体の力学的応答、例えば作用する応力と変形速度を結びつける式を構成方程式 (constitutive equation)という。運動量の保存則(1.4)に構成方程式を加えることで、流体の速度に関する閉じた方程式を構成することができる。

流体中の速度場から速度勾配テンソル(velocity gradient tensor) $L_{ij}$ を

L_{ij}=\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}

のように定義する。これを用いて2つのテンソル $\bm{E}$ と $\bm{W}$ を

	$\displaystyle\bm{E}=\frac{\displaystyle 1}{\displaystyle 2}\left(\bm{L}+\bm{L}% ^{T}\right)\quad\mathrm{or}\quad e_{ij}=\frac{\displaystyle 1}{\displaystyle 2% }\left(\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}+\frac{% \displaystyle\partial v_{j}}{\displaystyle\partial x_{i}}\right)$		(1.6)
	$\displaystyle\bm{W}=\frac{\displaystyle 1}{\displaystyle 2}\left(\bm{L}-\bm{L}% ^{T}\right)\quad\mathrm{or}\quad w_{ij}=\frac{\displaystyle 1}{\displaystyle 2% }\left(\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}-\frac{% \displaystyle\partial v_{j}}{\displaystyle\partial x_{i}}\right)$

のように定義する。 $\bm{W}$ は回転速度テンソルと呼ばれ、剛体的な回転を表わしている。一方、 $\bm{E}$ は歪速度テンソル(strain rate tensor)と呼ばれ、非剛体的な変形を表わす。この両者のうち、 $\bm{W}$ は(剛体回転を表わしているから)流体中の偏差応力には寄与しない。

多くの流体では、歪速度テンソル $e_{ij}$ と偏差応力テンソル $\tau_{ij}$ の間には線型な関係がある。このような流体をNewton流体と呼ぶ。さらに流体が等方的であるとすれば、 $e_{ij}$ と $\tau_{ij}$ は

\tau_{ij}=2\mu e_{ij}+\lambda e_{kk}\delta_{ij}

(1.7)

なる関係式で結ばれる。ここで $\delta_{ij}$ はKroneckerの $\delta$ であり、 $\mu$ は粘性率、 $\lambda$ は第2粘性率と呼ばれる。また偏差応力テンソル $\tau_{ij}$ の対角和(trace)をとり、空間の3方向に平均すると、

\frac{\displaystyle\tau_{ii}}{\displaystyle 3}=e_{ii}\left(\lambda+\frac{% \displaystyle 2}{\displaystyle 3}\mu\right)

(1.8)

となるが、ここで現れる $\lambda+\frac{\displaystyle 2}{\displaystyle 3}\mu$ を体積粘性率 (bulk viscosity) $k_{B}$ と呼び、 $k_{B}$ と書く。体積粘性率 $k_{B}$ は流体の体積変化に伴なう粘性応力の目安である。多くの流体では $k_{B}$ は非常に小さいことが知られているので、 $k_{B}=0$ とする (Stokes近似)。これより、Newton流体かつStokes流体の場合には、偏差応力テンソルの成分は

\tau_{ij}=2\mu e_{ij}-\frac{\displaystyle 2}{\displaystyle 3}\mu e_{kk}\delta_% {ij}=\mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}+% \frac{\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}}-\frac{% \displaystyle 2}{\displaystyle 3}\frac{\displaystyle\partial v_{k}}{% \displaystyle\partial x_{k}}\delta_{ij}\right)

(1.9)

となる。

式(1.9)を式(1.4)に代入すると、よく知られたNavier-Stokes 方程式

\rho\frac{\displaystyle Dv_{i}}{\displaystyle Dt}=-\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}+\frac{\displaystyle\partial}{\displaystyle% \partial x_{j}}\left[\mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle% \partial x_{j}}+\frac{\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}% }-\frac{\displaystyle 2}{\displaystyle 3}\frac{\displaystyle\partial v_{k}}{% \displaystyle\partial x_{k}}\delta_{ij}\right)\right]+\rho g_{i}

(1.10)

を得る。特に非圧縮を仮定すると、式(1.10)は

\rho\frac{\displaystyle Dv_{i}}{\displaystyle Dt}=-\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}+\frac{\displaystyle\partial}{\displaystyle% \partial x_{j}}\left[\mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle% \partial x_{j}}+\frac{\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}% }\right)\right]+\rho g_{i}

(1.11)

と簡単化される。さらに(マントル対流らしくはなくなるが)粘性率 $\mu$ が一定であるとすると

\rho\frac{\displaystyle Dv_{i}}{\displaystyle Dt}=-\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}+\mu\frac{\displaystyle\partial^{2}v_{i}}{% \displaystyle\partial x_{j}^{2}}+\rho g_{i}

(1.12)

と表わされる。

1.1.4 状態方程式

熱力学的考察によれば、物質の状態は2つの状態変数(温度 $T$ 、圧力 $p$ など)により定められる。即ち、状態方程式は一般的には3つの変数を含んだ式、例えば

f(p,\rho,T)=0

(1.13)

のように表わされる。

状態方程式を具体的に指定する際には、熱膨張率 $\alpha$ や等温圧縮率 $\chi_{T}$ を用いるのが便利である。これらは以下のように定義される。

\alpha\equiv\frac{\displaystyle 1}{\displaystyle V}\left(\frac{\displaystyle% \partial V}{\displaystyle\partial T}\right)_{p}=-\frac{\displaystyle 1}{% \displaystyle\rho}\left(\frac{\displaystyle\partial\rho}{\displaystyle\partial T% }\right)_{p}

(1.14)

\chi_{T}\equiv-\frac{\displaystyle 1}{\displaystyle V}\left(\frac{% \displaystyle\partial V}{\displaystyle\partial p}\right)_{T}=\frac{% \displaystyle 1}{\displaystyle\rho}\left(\frac{\displaystyle\partial\rho}{% \displaystyle\partial p}\right)_{T}

(1.15)

ここで、 $V=1/\rho$ は比体積である。上式で( )の右下つきの添字は、その変数を一定に保ったままの微分を表わす。

1.1.5 熱エネルギーの保存則

マントル対流で考慮すべきエネルギーには、熱エネルギーと運動エネルギーの2 種類があるが、ここでは熱エネルギーの保存則のみを考える。運動エネルギーの保存則は運動量の保存則から導かれるものなので、ここでは考えない。

熱力学の第2法則より、熱エネルギーの保存則は

\rho T\frac{\displaystyle Ds}{\displaystyle Dt}=\Phi-\frac{\displaystyle% \partial q_{i}}{\displaystyle\partial x_{i}}+\rho H

(1.16)

と表わされる。ここで、 $T$ は温度、 $s$ は比エントロピー(単位質量あたりのエントロピー)、 $H$ は単位質量あたりの内部加熱率である。右辺第1項は粘性散逸による発熱で、

\Phi=\tau_{ij}\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}

(1.17)

と書ける。また右辺第2項は伝導による熱輸送であり、熱流量 $\bm{q}$ はFourierの法則から

q_{i}=-k\frac{\displaystyle\partial T}{\displaystyle\partial x_{i}}

(1.18)

と表わされる。ここで $k$ は熱伝導率である。

粘性散逸 $\Phi$ をあらわに書くと、

	$\displaystyle\Phi$	$\displaystyle=\left[\mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle% \partial x_{j}}+\frac{\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}% }\right)+\left(k_{B}-\frac{\displaystyle 2}{\displaystyle 3}\mu\right)\frac{% \displaystyle\partial v_{k}}{\displaystyle\partial x_{k}}\delta_{ij}\right]% \frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}$
		$\displaystyle=k_{B}\left(\frac{\displaystyle\partial v_{i}}{\displaystyle% \partial x_{i}}\right)^{2}+2\mu\left[\frac{\displaystyle 1}{\displaystyle 2}% \left(\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}+\frac{% \displaystyle\partial v_{j}}{\displaystyle\partial x_{i}}\right)-\frac{% \displaystyle 1}{\displaystyle 3}\frac{\displaystyle\partial v_{k}}{% \displaystyle\partial x_{k}}\delta_{ij}\right]^{2}$		(1.19)

ここで右辺第1項は体積変化に起因する項、第2項は剪断変形(体積変化を伴なわない)に起因する項を表わす。さらにStokes近似( $k_{B}=0$ )かつ非圧縮性を仮定すれば、式(1.19)は

\Phi=\frac{\displaystyle\mu}{\displaystyle 2}\left(\frac{\displaystyle\partial v% _{i}}{\displaystyle\partial x_{j}}+\frac{\displaystyle\partial v_{j}}{% \displaystyle\partial x_{i}}\right)^{2}

(1.20)

と簡単化される。

式(1.16)の左辺を具体的にどう書き表わすかによって、熱エネルギーの保存則はさまざまな形で書き表わすことができる。導出の詳細は補遺Aを参照のこと。例えば、温度 $T$ と圧力 $p$ を独立変数として選ぶと、

ds=\frac{\displaystyle C_{p}}{\displaystyle T}dT-\frac{\displaystyle\alpha}{% \displaystyle\rho}dp

(1.21)

となる。ここで、 $C_{p}$ は定圧比熱である。これを式(1.16)に代入すれば

\rho C_{p}\frac{\displaystyle DT}{\displaystyle Dt}-\alpha T\frac{% \displaystyle Dp}{\displaystyle Dt}=\frac{\displaystyle\partial}{\displaystyle% \partial x_{i}}\left(k\frac{\displaystyle\partial T}{\displaystyle\partial x_{% i}}\right)+\Phi+\rho H

(1.22)

を得る。

1.2 マントル対流向けの近似

以下では、マントル内の熱対流を考える場合に有効な近似を導入し、前章で導出した基礎方程式を簡略化する。

まず、状態方程式(1.13)の簡単化を考える。マントル物質の相転移や組成の違いによる密度変化を無視すれば、マントルの密度 $\rho$ は第一義的には温度 $T$ と圧力 $p$ の関数で与えられる。

\rho=\rho(T,p)

密度変化は主に静水圧下の圧縮によるものが大きい(マントルの上面と下面で約65%程度)ことが知られている。これより、式を簡単にするため、 $\rho=\overline{\rho}+\rho\prime$ 、 $T=\overline{T}+T\prime$ 、 $p=\overline{p}+p\prime$ の如く、基本場 ( $\bar{~{}}$ つき)と基本場からのずれ( $\prime$ つき)の2つに分ける。

$\displaystyle\rho$	$\displaystyle=\overline{\rho}+\rho\prime=\rho(\overline{T}+T\prime,\overline{p% }+p\prime)$
	$\displaystyle\simeq\overline{\rho}(\overline{T},\overline{p})+\overline{\left(% \frac{\displaystyle\partial\rho}{\displaystyle\partial p}\right)_{T}}p\prime+% \overline{\left(\frac{\displaystyle\partial\rho}{\displaystyle\partial T}% \right)_{p}}T\prime$
	$\displaystyle=\overline{\rho}(\overline{T},\overline{p})+\overline{\rho}\,% \overline{\chi}_{T}\,p\prime-\overline{\alpha}\,\overline{\rho}\,T\prime$	(1.23)

その際、定常かつ運動のない状態を基本場として採用するのが便利である。さらに簡単のため、基本場の空間変化は重力の方向にのみ起こると仮定する。この仮定から、圧力の基本場が満たすべき式は

0=-\frac{\displaystyle\partial\overline{p}}{\displaystyle\partial x_{i}}+% \overline{\rho}\,\overline{g}_{i}

(1.24)

で与えられる。

以降は、式(1.23)を基にして、基礎方程式を簡略化していく。その際、方程式のスケーリングを行ない、各項の大きさを見積っていくのが便利である。表1及び2にスケーリングに用いる諸量をまとめておく。

Table 1: スケーリングに用いる基準量

記号	意味	値の目安
$\rho_{r}$	対流している状態での特徴的な密度	$4\times 10^{3}$ kg m^-3
$\Delta T_{r}$	対流を駆動する特徴的な温度差	$10^{3}$ K
${\chi_{T}}_{r}$	等温圧縮率 $\chi_{T}$ の基準値	$3\times 10^{-12}$ Pa^-1
$\alpha_{r}$	熱膨張率 $\alpha$ の基準値	$3\times 10^{-5}$ K^-1
$\mu_{r}$	粘性率 $\mu$ の基準値	$10^{21}$ Pa s
$k_{r}$	熱伝導率 $k$ の基準値	$4$ W m^-1K^-1
${C_{p}}_{r}$	定圧比熱 $C_{p}$ の基準値	$10^{3}$ J kg^-1K^-1
$b$	対流層の厚さ	$3\times 10^{6}$ m

Table 2: 基礎方程式の無次元化に用いるスケール

量	スケール	値の目安
長さ	$b$	$3\times 10^{6}$ m
時間	$b^{2}\rho_{r}{C_{p}}_{r}/k_{r}$	$9\times 10^{18}$ s
速度	$k_{r}/b\rho_{r}{C_{p}}_{r}$	$3.3\times 10^{-13}$ m s^-1
圧力	$\mu_{r}k_{r}/b^{2}\rho_{r}{C_{p}}_{r}$	$1.1\times 10^{2}$ Pa

以下では、無次元化された量を^∗で表記する。

線型化された状態方程式(1.23)をスケーリングすると、

	$\displaystyle\frac{\displaystyle\rho^{\ast}}{\displaystyle\overline{\rho}^{% \ast}}$	$\displaystyle=1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle k_% {r}\mu_{r}{\chi_{T}}_{r}}{\displaystyle\rho_{r}{C_{p}}_{r}b^{2}}-\overline{% \alpha}^{\ast}T\prime^{\ast}\,\alpha_{r}\Delta T_{r}$
		$\displaystyle=1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-\overline{% \alpha}^{\ast}T\prime^{\ast}\epsilon$		(1.25)

ここで新たに3つの無次元量を定義した。

M^{2}\equiv\frac{\displaystyle k_{r}^{2}{\chi_{T}}_{r}}{\displaystyle\rho_{r}{% C_{p}}_{r}^{2}b^{2}},\quad Pr\equiv\frac{\displaystyle\mu_{r}{C_{p}}_{r}}{% \displaystyle k_{r}},\quad\epsilon\equiv\alpha_{r}\Delta T_{r}

(1.26)

$M$ はMach数(系の特徴的な速度と音速の比)、 $P r$ はPrantdl数(運動量の拡散率と熱拡散率の比)であり、 $\epsilon$ は熱的な浮力の目安を表わす。表1の値を用いると、これらの無次元量は $M^{2}\sim 10^{-33}$ 、 $Pr\sim 2.5\times 10^{23}$ 、 $\epsilon\sim 3\times 10^{-2}$ と推定できる。これより、式(1.25)内で $M^{2}Pr$ や $\epsilon$ を含む項を無視してもよいことが理解できる。 $M^{2}Pr\rightarrow 0$ かつ $\epsilon\rightarrow 0$ とおく近似を非弾性近似 (anelastic approximation) という。

次に質量保存則(1.1)をスケーリングする。スケーリングされた状態方程式(1.25)を代入して整理すると、

\overline{\rho}^{\ast}\left(\overline{\chi}^{\ast}M^{2}Pr\frac{\displaystyle% \partial p\prime^{\ast}}{\displaystyle\partial t^{\ast}}-\overline{\alpha}^{% \ast}\epsilon\frac{\displaystyle\partial T\prime^{\ast}}{\displaystyle\partial t% ^{\ast}}\right)+\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast% }}\left[\overline{\rho}^{\ast}\left(1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}% M^{2}Pr-\overline{\alpha}^{\ast}T\prime^{\ast}\epsilon\right)v_{i}^{\ast}% \right]=0

(1.27)

式(1.27)に非弾性近似を適用すると

\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}\left(% \overline{\rho}^{\ast}v_{i}^{\ast}\right)=0

(1.28)

を得る。この式は $\rho\prime^{\ast}$ の時間変化を無視したことになっており、これにより基礎方程式から弾性波を除去することができる。実際、マントル内の弾性波(要するに地震波)は数km/秒で伝播する現象であり、マントル対流が対象とする時間スケール(数百万年以上)では当然除去すべきものである。さらに、 $\overline{\rho}^{\ast}$ の空間変化が無視できる(Boussinesq近似)と仮定すれば、式(1.28)は

\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle\partial x_{i}^{\ast}}=0

(1.29)

となり、非圧縮性流体の条件と一致する。

ここで、Boussinesq近似の意味を考えてみる。断熱的な場合における $\overline{\rho}$ の空間変化は

\frac{\displaystyle\partial\overline{\rho}}{\displaystyle\partial x_{i}}=% \overline{\left(\frac{\displaystyle\partial\rho}{\displaystyle\partial p}% \right)_{s}}\left(\frac{\displaystyle\partial p}{\displaystyle\partial x_{i}}% \right)=\overline{\rho}\,\overline{\chi_{a}}\left(\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}\right)

ここで $\chi_{a}$ は断熱圧縮率である。圧力の空間変化が静水圧的であると仮定すると、

\frac{\displaystyle\partial\overline{\rho}}{\displaystyle\partial x_{i}}=% \overline{\rho}\,\overline{\chi_{a}}\,\overline{\rho}\,\overline{g}_{i}=% \overline{\rho}^{2}\,\overline{\chi_{a}}\,\overline{g}_{i}

(1.30)

式(1.30)から、 $\overline{\rho}$ の変化が起こる空間スケール $\overline{h_{d}}$ を見積ると、

	$\displaystyle\overline{h_{d}}$	$\displaystyle=\left[\frac{\displaystyle 1}{\displaystyle\overline{\rho}}\left\|% \frac{\displaystyle\partial\overline{\rho}}{\displaystyle\partial x_{i}}\right% \|\right]^{-1}$		(1.31)
		$\displaystyle=\frac{\displaystyle 1}{\displaystyle\overline{\rho}\,\overline{% \chi_{a}}\,\overline{g}}=\frac{\displaystyle\overline{\gamma}\,\overline{C_{p}% }}{\displaystyle\overline{\alpha}\,\overline{g}}$		(1.32)

ここで、Grüneisen parameter $\gamma$

\gamma=\frac{\displaystyle\alpha}{\displaystyle\rho C_{v}\chi_{T}}=\frac{% \displaystyle\alpha}{\displaystyle\rho C_{p}\chi_{a}}

(1.33)

を導入した。式(1.32)で定義された $\overline{h_{d}}$ が $b$ よりも十分大きければ、 $\overline{\rho}$ の空間変化を無視してもよいであろう。即ち、

1\gg\frac{\displaystyle b}{\displaystyle\overline{h_{d}}}=\frac{\displaystyle b% \overline{\alpha}\,\overline{g}}{\displaystyle\overline{\gamma}\,\overline{C_{% p}}}

右辺をスケーリングしてやると

1\gg\frac{\displaystyle\overline{\alpha}^{\ast}\overline{g}^{\ast}}{% \displaystyle\overline{\gamma}^{\ast}\overline{C_{p}}^{\ast}}\frac{% \displaystyle\alpha_{r}g_{r}b}{\displaystyle\gamma_{r}{C_{p}}_{r}}=\frac{% \displaystyle\overline{\alpha}^{\ast}\overline{g}^{\ast}}{\displaystyle% \overline{\gamma}^{\ast}\overline{C_{p}}^{\ast}}\frac{\displaystyle D}{% \displaystyle\gamma_{r}}

(1.34)

ここで

D\equiv\frac{\displaystyle\alpha_{r}g_{r}b}{\displaystyle{C_{p}}_{r}}

(1.35)

はDissipation numberと呼ばれる量である。 Dissipation number と Grüneisen parameter の比 $D/\gamma_{r}$ はマントルの厚さとマントル内の密度変化の空間スケールとの比を表わす。式(1.34)より、Boussinesq近似とは、 $D/\gamma_{r}\rightarrow 0$ とした極限に相当する。しかし、実際のマントルでは $D\sim 0.5$ 、 $\gamma\sim 1$ と見積られる。 Boussinesq近似は式が簡便なためよく用いられるが、実際はその程度でしか正しくないことに注意しよう。

Navier-Stokes方程式(1.10)のスケーリングを行なう。スケーリングされた状態方程式(1.25)を代入して整理すると、

	$\displaystyle\frac{\displaystyle 1}{\displaystyle Pr}\overline{\rho}^{\ast}% \left(1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-\overline{\alpha}^{% \ast}T\prime^{\ast}\epsilon\right)\frac{\displaystyle Dv_{i}^{\ast}}{% \displaystyle Dt^{\ast}}$	$\displaystyle=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\frac{\displaystyle\partial}{\displaystyle\partial x_{j% }^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{% \displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{% \displaystyle\partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}% \frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}% \delta_{ij}\right)\right]$
		$\displaystyle+\rho_{r}{\chi_{T}}_{r}g_{r}b\,\overline{g}_{i}^{\ast}\overline{% \rho}^{\ast}\overline{\chi}_{T}^{\ast}p\prime^{\ast}-\frac{\displaystyle b^{3}% \rho_{r}^{2}{C_{p}}_{r}g_{r}\alpha_{r}{\Delta T}_{r}}{\displaystyle\mu_{r}k_{r% }}\overline{\rho}^{\ast}\overline{\alpha}^{\ast}\overline{g}_{i}^{\ast}T\prime% ^{\ast}$

式(1.33)と(1.35)より、右辺第3項は

\frac{\displaystyle D}{\displaystyle\gamma_{r}}\frac{\displaystyle{C_{p}}_{r}}% {\displaystyle{C_{v}}_{r}}\,\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}% \overline{\chi}_{T}^{\ast}p\prime^{\ast}

となり、右辺第4項から新たな無次元量 $R a$ を

Ra\equiv\frac{\displaystyle b^{3}\rho_{r}^{2}{C_{p}}_{r}g_{r}\alpha_{r}{\Delta T% }_{r}}{\displaystyle\mu_{r}k_{r}}

(1.36)

と定義する。 $R a$ はRayleigh数と呼ばれる。これらを用いると、スケーリングされたNavier-Stokes方程式は結局

	$\displaystyle\frac{\displaystyle 1}{\displaystyle Pr}\overline{\rho}^{\ast}% \left(1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-\overline{\alpha}^{% \ast}T\prime^{\ast}\epsilon\right)\frac{\displaystyle Dv_{i}^{\ast}}{% \displaystyle Dt^{\ast}}$	$\displaystyle=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}\overline{% \chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle D}{\displaystyle\gamma_{r}}% \frac{\displaystyle{C_{p}}_{r}}{\displaystyle{C_{v}}_{r}}$
		$\displaystyle-\overline{\rho}^{\ast}\overline{\alpha}^{\ast}\overline{g}_{i}^{% \ast}T\prime^{\ast}\,Ra+\frac{\displaystyle\partial}{\displaystyle\partial x_{% j}^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{% \displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{% \displaystyle\partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}% \frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}% \delta_{ij}\right)\right]$		(1.37)

となる。ここで $1/Pr\rightarrow 0$ であることを考えると、式(1.37)の左辺は無視することができる。これより、非弾性近似を適用した場合には式(1.37)は

	$\displaystyle 0=$	$\displaystyle-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}\overline{% \chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle D}{\displaystyle\gamma_{r}}% \frac{\displaystyle{C_{p}}_{r}}{\displaystyle{C_{v}}_{r}}-\overline{\rho}^{% \ast}\overline{\alpha}^{\ast}\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra$
		$\displaystyle+\frac{\displaystyle\partial}{\displaystyle\partial x_{j}^{\ast}}% \left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle% \partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}\frac{% \displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}\delta_% {ij}\right)\right]$		(1.38)

となる。式(1.38)の右辺より、対流を駆動する浮力には、(i)温度変化による密度変化(第3項)、及び (ii) 圧力変化による密度変化(第2項)、の2つの寄与があることが分かる。しかし一般的には、(ii) の寄与を無視して、

\displaystyle 0=

\displaystyle-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\overline{\rho}^{\ast}\overline{\alpha}^{\ast}\overline% {g}_{i}^{\ast}T\prime^{\ast}\,Ra+\frac{\displaystyle\partial}{\displaystyle% \partial x_{j}^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^% {\ast}}{\displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^% {\ast}}{\displaystyle\partial x_{i}^{\ast}}-\frac{\displaystyle 2}{% \displaystyle 3}\frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle% \partial x_{k}^{\ast}}\delta_{ij}\right)\right]

(1.39)

とした方程式を用いることが多い。これを「打ち切りされた非弾性近似 (truncated anelasic liquid approximation)」と呼ぶ。この場合、浮力に寄与するのは温度変化による密度変化のみになる。さらに、Boussinesq近似を施すと、

0=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle\partial x_{i}^{% \ast}}-\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra+\frac{\displaystyle\partial}{% \displaystyle\partial x_{j}^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle% \partial v_{i}^{\ast}}{\displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle% \partial v_{j}^{\ast}}{\displaystyle\partial x_{i}^{\ast}}\right)\right]

(1.40)

と簡単化される。ただしここでは Boussinesq 近似を利用して、 $\overline{\rho}^{\ast}=\overline{\alpha}^{\ast}=\textrm{const.}\equiv 1$ かつ $\frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}=0$ を用いた。

最後に、熱エネルギーの保存則(1.22)式のスケーリングを行なう。スケーリングされた状態方程式(1.25)を代入して整理すると、

	$\displaystyle\overline{\rho}^{\ast}\left(1+\overline{\chi}_{T}^{\ast}p\prime^{% \ast}M^{2}Pr-\overline{\alpha}^{\ast}T\prime^{\ast}\epsilon\right)\overline{C_% {p}}^{\ast}\frac{\displaystyle D}{\displaystyle Dt^{\ast}}\left(\overline{T}^{% \ast}+T\prime^{\ast}\right)-\underbrace{\frac{\displaystyle\alpha_{r}\mu_{r}k_% {r}}{\displaystyle b^{2}\rho_{r}^{2}{C_{p}}_{r}^{2}}}_{=\frac{\displaystyle% \epsilon D}{\displaystyle Ra}}\overline{\alpha}^{\ast}\left(\overline{T}^{\ast% }+T\prime^{\ast}\right)\frac{\displaystyle D}{\displaystyle Dt^{\ast}}\left(% \overline{p}^{\ast}+p\prime^{\ast}\right)$
	$\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[\overline{k}^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_% {i}^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]+\underbrace{% \frac{\displaystyle\mu_{r}k_{r}}{\displaystyle b^{2}\rho_{r}^{2}{C_{p}}_{r}^{2% }\Delta T_{r}}}_{=\frac{\displaystyle D}{\displaystyle Ra}}\Phi^{\ast}+% \overline{\rho}^{\ast}\left(1+\overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-% \overline{\alpha}^{\ast}T\prime^{\ast}\epsilon\right)H^{\ast}\left(\frac{% \displaystyle b^{2}H_{r}\rho_{r}}{\displaystyle k_{r}\Delta T_{r}}\right)$

ここで、内部発熱率の基準値 $H_{r}$ を導入した。さらに左辺第2項に含まれる、圧力の基本場 $\overline{p}^{\ast}$ のLagrange微分の項を変形する。基本場は時間変化しないと仮定しているので、

\frac{\displaystyle D\overline{p}^{\ast}}{\displaystyle Dt^{\ast}}=\frac{% \displaystyle\partial\overline{p}^{\ast}}{\displaystyle\partial t^{\ast}}+v_{i% }^{\ast}\frac{\displaystyle\partial\overline{p}^{\ast}}{\displaystyle\partial x% _{i}^{\ast}}=v_{i}^{\ast}\frac{\displaystyle\partial\overline{p}^{\ast}}{% \displaystyle\partial x_{i}^{\ast}}

一方、式(1.24)をスケーリングすると

\frac{\displaystyle\partial\overline{p}^{\ast}}{\displaystyle\partial x_{i}^{% \ast}}=\frac{\displaystyle b^{3}\rho_{r}^{2}{C_{p}}_{r}g_{r}}{\displaystyle\mu% _{r}k_{r}}\overline{\rho}^{\ast}\overline{g}_{i}^{\ast}=\frac{\displaystyle Ra% }{\displaystyle\epsilon}\overline{\rho}^{\ast}\overline{g}_{i}^{\ast}

であるから結局

\frac{\displaystyle D\overline{p}^{\ast}}{\displaystyle Dt^{\ast}}=\frac{% \displaystyle Ra}{\displaystyle\epsilon}\overline{\rho}^{\ast}\overline{g}_{i}% ^{\ast}v_{i}^{\ast}

これを代入して整理すると、スケーリングされた熱エネルギーの保存則は結局、

	$\displaystyle\overline{\rho}^{\ast}\left(1+\overline{\chi}_{T}^{\ast}p\prime^{% \ast}M^{2}Pr-\overline{\alpha}^{\ast}T\prime^{\ast}\epsilon\right)\overline{C_% {p}}^{\ast}\frac{\displaystyle D}{\displaystyle Dt^{\ast}}\left(\overline{T}^{% \ast}+T\prime^{\ast}\right)-\overline{\alpha}^{\ast}\left(\overline{T}^{\ast}+% T\prime^{\ast}\right)\frac{\displaystyle Dp\prime^{\ast}}{\displaystyle Dt^{% \ast}}\frac{\displaystyle\epsilon D}{\displaystyle Ra}-\overline{\alpha}^{\ast% }\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\overline{g}_{i}^{\ast}v_{i}^{% \ast}\overline{\rho}^{\ast}D$
	$\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[\overline{k}^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_% {i}^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]+\Phi^{\ast}% \frac{\displaystyle D}{\displaystyle Ra}+\overline{\rho}^{\ast}\left(1+% \overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-\overline{\alpha}^{\ast}T% \prime^{\ast}\epsilon\right)H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho_{% r}}{\displaystyle k_{r}\Delta T_{r}}\right)$		(1.41)

これに非弾性近似を適用すると、

\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle D% }{\displaystyle Dt^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)-% \overline{\alpha}^{\ast}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)% \overline{g}_{i}^{\ast}v_{i}^{\ast}\overline{\rho}^{\ast}D=\frac{\displaystyle% \partial}{\displaystyle\partial x_{i}^{\ast}}\left[\overline{k}^{\ast}\frac{% \displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}\left(\overline{T}^{% \ast}+T\prime^{\ast}\right)\right]+\Phi^{\ast}\frac{\displaystyle D}{% \displaystyle Ra}+\overline{\rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2% }H_{r}\rho_{r}}{\displaystyle k_{r}\Delta T_{r}}\right)

(1.42)

を得る。

温度の基本場 $\overline{T}^{\ast}$ をしかるべく仮定すると、式(1.42) はさらに簡単化できる。基本場は時間変化しないと仮定しているので、

\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle D\overline{T}% ^{\ast}}{\displaystyle Dt^{\ast}}=\overline{\rho}^{\ast}\overline{C_{p}}^{\ast% }v_{i}^{\ast}\frac{\displaystyle\partial\overline{T}^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}

加えて、基本場は断熱的であると仮定すると、断熱温度勾配の式(A.19) をスケーリングすることにより、

\frac{\displaystyle\partial\overline{T}^{\ast}}{\displaystyle\partial x_{i}^{% \ast}}=\frac{\displaystyle\alpha_{r}g_{r}b}{\displaystyle{C_{p}}_{r}}\frac{% \displaystyle\overline{\alpha}^{\ast}\overline{g}_{i}^{\ast}}{\displaystyle% \overline{C_{p}}^{\ast}}\overline{T}^{\ast}=D\frac{\displaystyle\overline{% \alpha}^{\ast}\overline{g}_{i}^{\ast}}{\displaystyle\overline{C_{p}}^{\ast}}% \overline{T}^{\ast}

となる。これより、

\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle D\overline{T}% ^{\ast}}{\displaystyle Dt^{\ast}}=\overline{\rho}^{\ast}\overline{\alpha}^{% \ast}\overline{T}^{\ast}D\overline{g}_{i}^{\ast}v_{i}^{\ast}

(1.43)

が得られる。式(1.43)を式(1.42)に代入してやると、非弾性近似における熱エネルギーの保存則

\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}-\overline{\alpha}^{\ast}T\prime^{\ast}% \overline{g}_{i}^{\ast}v_{i}^{\ast}\overline{\rho}^{\ast}D=\frac{\displaystyle% \partial}{\displaystyle\partial x_{i}^{\ast}}\left[\overline{k}^{\ast}\frac{% \displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}\left(\overline{T}^{% \ast}+T\prime^{\ast}\right)\right]+\Phi^{\ast}\frac{\displaystyle D}{% \displaystyle Ra}+\overline{\rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2% }H_{r}\rho_{r}}{\displaystyle k_{r}\Delta T_{r}}\right)

(1.44)

が得られる。左辺第2項が断熱温度勾配に沿った温度変化の効果を表わしている。加えて熱伝導率などが一様であると仮定すれば、右辺第1項内の熱伝導項を簡単にすることもできる。さらにBoussinesq近似を適用すると、 $D\rightarrow 0$ の場合には断熱温度勾配が0になるので、

\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}=\frac{\displaystyle\partial}{% \displaystyle\partial x_{i}^{\ast}}\left(\overline{k}^{\ast}\frac{% \displaystyle\partial T\prime^{\ast}}{\displaystyle\partial x_{i}^{\ast}}% \right)+\overline{\rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho% _{r}}{\displaystyle k_{r}\Delta T_{r}}\right)

(1.45)

となる。

以上で、マントル対流向けの基礎方程式系の近似が完了した。

これまでに適用した非弾性近似とBoussinesq近似の他に、マントル対流シミュレーションには「拡張されたBoussinesq近似」(extended Boussinesq approximation) なる近似が使われることもある。この近似は、Boussinesq近似で課された $D/\gamma_{r}\rightarrow 0$ の条件を $D\rightarrow 0$ ではなく、 $\gamma\rightarrow\infty$ かつ $D\not=0$ として適用するものである。この場合、質量保存則と Navier-Stokes方程式はBoussinesq近似によるもの(式 (1.3)及び(1.40))と同じになり、熱エネルギー保存則は非弾性近似によるもの(式(1.44))を用いることになる。

1.2.1 てっとり早く知りたい方のための基礎方程式のまとめ

1.
基礎方程式の一般形 (次元つき)
- •
  
  質量保存則
  
  $\frac{\displaystyle 1}{\displaystyle\rho}\frac{\displaystyle D\rho}{% \displaystyle Dt}+\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{% i}}=0$ (1.2)
- •
  
  運動量保存則 (Navier-Stokes 方程式)
  
  $\rho\frac{\displaystyle Dv_{i}}{\displaystyle Dt}=-\frac{\displaystyle\partial p% }{\displaystyle\partial x_{i}}+\frac{\displaystyle\partial}{\displaystyle% \partial x_{j}}\left[\mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle% \partial x_{j}}+\frac{\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}% }-\frac{\displaystyle 2}{\displaystyle 3}\frac{\displaystyle\partial v_{k}}{% \displaystyle\partial x_{k}}\delta_{ij}\right)\right]+\rho g_{i}$ (1.10)
- •
  
  熱エネルギー保存則
  
  $\rho C_{p}\frac{\displaystyle DT}{\displaystyle Dt}-\alpha T\frac{% \displaystyle Dp}{\displaystyle Dt}=\frac{\displaystyle\partial}{\displaystyle% \partial x_{i}}\left(k\frac{\displaystyle\partial T}{\displaystyle\partial x_{% i}}\right)+\Phi+\rho H$ (1.22)

非弾性近似 ( $\epsilon\ll 1$ , $M^{2}Pr\ll 1$ ) かつPrandtl数無限大の場合 (次元なし)

•

基本場は運動なし、定常、静水圧的、かつ断熱的とした
•

質量保存則

$\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}\left(% \overline{\rho}^{\ast}v_{i}^{\ast}\right)=0$ (1.28)

•

運動量保存則 (Navier-Stokes 方程式)

	$\displaystyle 0=$	$\displaystyle-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}\overline{% \chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle D}{\displaystyle\gamma_{r}}% \frac{\displaystyle{C_{p}}_{r}}{\displaystyle{C_{v}}_{r}}-\overline{\rho}^{% \ast}\overline{\alpha}^{\ast}\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra$
		$\displaystyle+\frac{\displaystyle\partial}{\displaystyle\partial x_{j}^{\ast}}% \left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle% \partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}\frac{% \displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}\delta_% {ij}\right)\right]$		(1.38)

•

熱エネルギー保存則

$\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}-\overline{\alpha}^{\ast}T\prime^{\ast}% \overline{g}_{i}^{\ast}v_{i}^{\ast}\overline{\rho}^{\ast}D$ $\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[\overline{k}^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_% {i}^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]$

$\displaystyle+\Phi^{\ast}\frac{\displaystyle D}{\displaystyle Ra}+\overline{% \rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho_{r}}{% \displaystyle k_{r}\Delta T_{r}}\right)$ (1.44)

ちなみに、次元つきの量に戻して書き直すと以下のようになる。

•

質量保存則

$\frac{\displaystyle\partial}{\displaystyle\partial x_{i}}\left(\overline{\rho}% v_{i}\right)=0$ (1.46)
•

運動量保存則 (Navier-Stokes 方程式)

$\displaystyle 0=$ $\displaystyle-\frac{\displaystyle\partial p\prime}{\displaystyle\partial x_{i}% }+\overline{\rho}\overline{g}_{i}\left(\overline{\chi}_{T}p\prime-\overline{% \alpha}T\prime\right)$

$\displaystyle+\frac{\displaystyle\partial}{\displaystyle\partial x_{j}}\left[% \mu\left(\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{j}}+\frac% {\displaystyle\partial v_{j}}{\displaystyle\partial x_{i}}-\frac{\displaystyle 2% }{\displaystyle 3}\frac{\displaystyle\partial v_{k}}{\displaystyle\partial x_{% k}}\delta_{ij}\right)\right]$ (1.47)
•

熱エネルギー保存則

$\displaystyle\overline{\rho}\overline{C_{p}}\frac{\displaystyle DT\prime}{% \displaystyle Dt}-\overline{\alpha}T\prime\overline{g}_{i}v_{i}\overline{\rho}$ $\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}}\left[% \overline{k}\frac{\displaystyle\partial}{\displaystyle\partial x_{i}}\left(% \overline{T}+T\prime\right)\right]+\Phi+\overline{\rho}H$ (1.48)

3.
打ち切りされた非弾性近似 ( $\epsilon\ll 1$ , $M^{2}Pr\ll 1$ , 圧力変化に起因する浮力を無視) かつ Prandtl数無限大の場合 (次元なし)
- •
  
  基本場は運動なし、定常、静水圧的、かつ断熱的とした
- •
  
  質量保存則
  
  $\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}\left(% \overline{\rho}^{\ast}v_{i}^{\ast}\right)=0$ (1.28)
- •
  
  運動量保存則 (Navier-Stokes 方程式)
  
  $\displaystyle 0=$ $\displaystyle-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\overline{\rho}^{\ast}\overline{\alpha}^{\ast}\overline% {g}_{i}^{\ast}T\prime^{\ast}\,Ra+\frac{\displaystyle\partial}{\displaystyle% \partial x_{j}^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^% {\ast}}{\displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^% {\ast}}{\displaystyle\partial x_{i}^{\ast}}-\frac{\displaystyle 2}{% \displaystyle 3}\frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle% \partial x_{k}^{\ast}}\delta_{ij}\right)\right]$ (1.38)
- •
  
  熱エネルギー保存則
  
  $\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}-\overline{\alpha}^{\ast}T\prime^{\ast}% \overline{g}_{i}^{\ast}v_{i}^{\ast}\overline{\rho}^{\ast}D$ $\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[\overline{k}^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_% {i}^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]$
  
  $\displaystyle+\Phi^{\ast}\frac{\displaystyle D}{\displaystyle Ra}+\overline{% \rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho_{r}}{% \displaystyle k_{r}\Delta T_{r}}\right)$ (1.44)
4.
Boussinesq 近似 ( $\epsilon\ll 1$ , $M^{2}Pr\ll 1$ , $D\ll 1$ ) かつ Prandtl数無限大の場合 (次元なし)
- •
  
  基本場は運動なし、定常、 $\overline{\rho}$ , $\overline{C}_{p}$ , $\overline{\alpha}$ が一定
- •
  
  質量保存則
  
  $\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle\partial x_{i}^{\ast}}=0$ (1.29)
- •
  
  運動量保存則 (Navier-Stokes 方程式)
  
  $0=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle\partial x_{i}^{% \ast}}-\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra+\frac{\displaystyle\partial}{% \displaystyle\partial x_{j}^{\ast}}\left[\mu^{\ast}\left(\frac{\displaystyle% \partial v_{i}^{\ast}}{\displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle% \partial v_{j}^{\ast}}{\displaystyle\partial x_{i}^{\ast}}\right)\right]$ (1.40)
- •
  
  熱エネルギー保存則
  
  $\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}=\frac{\displaystyle\partial}{% \displaystyle\partial x_{i}^{\ast}}\left(\overline{k}^{\ast}\frac{% \displaystyle\partial T\prime^{\ast}}{\displaystyle\partial x_{i}^{\ast}}% \right)+\overline{\rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho% _{r}}{\displaystyle k_{r}\Delta T_{r}}\right)$ (1.45)
ちなみに、次元つきの量に戻して書き直すと以下のようになる。
- •
  
  質量保存則
  
  $\frac{\displaystyle\partial v_{i}}{\displaystyle\partial x_{i}}=0$ (1.29)
- •
  
  運動量保存則 (Navier-Stokes 方程式)
  
  $0=-\frac{\displaystyle\partial p\prime}{\displaystyle\partial x_{i}}-\overline% {\rho}\,\overline{g}_{i}\overline{\alpha}T\prime+\frac{\displaystyle\partial}{% \displaystyle\partial x_{j}}\left[\mu\left(\frac{\displaystyle\partial v_{i}}{% \displaystyle\partial x_{j}}+\frac{\displaystyle\partial v_{j}}{\displaystyle% \partial x_{i}}\right)\right]$ (1.40)
- •
  
  熱エネルギー保存則
  
  $\displaystyle\overline{\rho}\overline{C_{p}}\frac{\displaystyle DT\prime}{% \displaystyle Dt}=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}}% \left(\overline{k}\frac{\displaystyle\partial T\prime}{\displaystyle\partial x% _{i}}\right)+\overline{\rho}H$ (1.45)

ただし、以下の無次元パラメータを含んでいる。

$\displaystyle Pr$	$\displaystyle=\mathrm{Prandtl~{}number}$	$\displaystyle\equiv\frac{\displaystyle\mu_{r}{C_{p}}_{r}}{\displaystyle k_{r}}$	(1.26)
$\displaystyle\epsilon$		$\displaystyle\equiv\alpha_{r}\Delta T_{r}$	(1.26)
$\displaystyle M^{2}$		$\displaystyle\equiv\frac{\displaystyle k_{r}^{2}{\chi_{T}}_{r}}{\displaystyle% \rho_{r}{C_{p}}_{r}^{2}b^{2}}$	(1.26)
$\displaystyle D$	$\displaystyle=\mathrm{Dissipation~{}number}$	$\displaystyle\equiv\frac{\displaystyle\alpha_{r}g_{r}b}{\displaystyle{C_{p}}_{% r}}$	(1.35)
$\displaystyle Ra$	$\displaystyle=\mathrm{Rayleigh~{}number}$	$\displaystyle\equiv\frac{\displaystyle b^{3}\rho_{r}^{2}{C_{p}}_{r}g_{r}\alpha% _{r}{\Delta T}_{r}}{\displaystyle\mu_{r}k_{r}}$	(1.36)
$\displaystyle Ra_{H}$	$\displaystyle=\mathrm{internal~{}heating~{}Rayleigh~{}number}$	$\displaystyle\equiv\frac{\displaystyle b^{5}\rho_{r}^{3}{C_{p}}_{r}g_{r}\alpha% _{r}H_{r}}{\displaystyle\mu_{r}k_{r}^{2}}$	(1.49)

1.3 マントル対流の基本場の設定

ここでは、先の導出では十分に検討しなかった、基本場の設定について論じる。以下のいずれの場合も、運動がなく静水圧的で、かつ定常な状態を基本場とする。

基本場とは、基礎方程式の扱いを容易にするための数学的な方便の一つというべきものであるので、必ずしも現実に存在しなくてもよい。しかしながら、特に圧縮性を考える際には注意が必要である。なぜなら、状態方程式を指定するのみならず、必要な熱力学変数を正しく (熱力学に則って) 扱う必要があるからである。

1.3.1 Boussinesq 近似の場合

Boussinesq 近似の場合には、基本場の設定は極めて簡単である。その理由の1つは、基本場での密度分布 $\overline{\rho}$ を一定とみなしてよいからである。

まず基本場での圧力分布を考えてみよう。そのためには静水圧を記述する式(1.24)を積分すればよい。式(1.24)の積分には重力加速度が必要だが、デカルト座標系の場合にはこれを一定とみなしてもよいであろうから、結局

\overline{p}=\overline{\rho}\,\overline{g}z

と書ける。ここで重力は $z$ 軸の正の向きに働くものとし、かつ $\overline{p}(z=0)=0$ とした。一方、3次元球殻モデルを考える場合には、半径方向に重力加速度が変化することを考慮する必要があるであろう。例えば外径 $a$ 、内径 $c$ の3次元球殻領域をとり、マントルの密度を $\rho_{m}$ 、コアの密度を $\rho_{c}$ とすると

	$\displaystyle\overline{g}(r)=\frac{\displaystyle G\overline{M}(r)}{% \displaystyle r^{2}}$	$\displaystyle=\frac{\displaystyle 4}{\displaystyle 3}\pi\rho_{c}Gr\quad(% \mathrm{for~{}}0\leq r\leq c)$		(1.50)
		$\displaystyle=\frac{\displaystyle 4}{\displaystyle 3}\pi G\left[r\rho_{m}+% \frac{\displaystyle c^{3}}{\displaystyle r^{2}}(\rho_{c}-\rho_{m})\right]\quad% (\mathrm{for~{}}c\leq r\leq a)$		(1.51)

となる。またこの場合の静水圧を記述する式は

\frac{\displaystyle d\overline{p}}{\displaystyle dr}=-\overline{\rho}\,% \overline{g}(r)

(1.52)

となるから、(1.51)と(1.52)より

	$\displaystyle\overline{p}(r)$	$\displaystyle=\frac{\displaystyle 4}{\displaystyle 3}\pi\rho_{m}Gc^{3}(\rho_{c% }-\rho_{m})\left(\frac{\displaystyle 1}{\displaystyle r}-\frac{\displaystyle 1% }{\displaystyle a}\right)+\frac{\displaystyle 2}{\displaystyle 3}\pi G\rho_{m}% ^{2}(a^{2}-r^{2})\quad(\mathrm{for~{}}c\leq r\leq a)$
		$\displaystyle=\frac{\displaystyle 2}{\displaystyle 3}\pi G\rho_{c}^{2}(c^{2}-r% ^{2})+\frac{\displaystyle 2}{\displaystyle 3}\pi G\rho_{m}^{2}(a^{2}-c^{2})+% \frac{\displaystyle 4}{\displaystyle 3}\pi\rho_{m}Gc^{3}(\rho_{c}-\rho_{m})% \left(\frac{\displaystyle 1}{\displaystyle c}-\frac{\displaystyle 1}{% \displaystyle a}\right)\quad(\mathrm{for~{}}0\leq r\leq c)$		(1.53)

を得る。ただしここでも $\overline{p}(r=a)=0$ とした。

次に温度の基本場について考える。 Boussinesq 近似では断熱温度勾配が0であるから、 $\overline{T}$ を一定にとるのが最も簡単である。しかしこれとは異なる $\overline{T}$ を採用することも可能である。例えば

0=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}}\left(\overline{k}% \frac{\displaystyle\partial\overline{T}}{\displaystyle\partial x_{i}}\right)+% \overline{\rho}H

(1.54)

で与えられる1次元定常熱伝導状態の解をとることもできる。デカルト座標系のもとで具体的に書くと

\displaystyle 0=\frac{\displaystyle d}{\displaystyle dz}\left(\overline{k}% \frac{\displaystyle d\overline{T}}{\displaystyle dz}\right)+\overline{\rho}H

(1.55)

あるいは3次元球殻モデルでは

\displaystyle 0=\frac{\displaystyle 1}{\displaystyle r^{2}}\frac{\displaystyle d% }{\displaystyle dr}\left(r^{2}\overline{k}\frac{\displaystyle d\overline{T}}{% \displaystyle dr}\right)+\overline{\rho}H

(1.56)

である。これに加えて $\overline{k}$ と $H$ の関数形を与えれば $\overline{T}$ が求まる。例えば $\overline{k}$ と $H$ の両方とも一定であるとすれば簡単に積分できて結局、

	$\displaystyle T(z)$	$\displaystyle=-\frac{\displaystyle\overline{\rho}H}{\displaystyle 2\overline{k% }}z^{2}+c_{1}z+c_{2}$		(1.57)
	$\displaystyle T(r)$	$\displaystyle=-\frac{\displaystyle\overline{\rho}H}{\displaystyle 6\overline{k% }}z^{2}+\frac{\displaystyle c_{1}}{\displaystyle r}+c_{2}$		(1.58)

を得る。ここで $c_{1}$ 及び $c_{2}$ は境界条件によって決まる積分定数である。

1.3.2 非Boussinesq近似の場合

次に圧縮性流体あるいは非弾性流体の場合を考える。この場合は、密度 $\rho$ や熱膨張率 $\alpha$ などの物性値の深さ(圧力)変化を自然に取り込める利点はあるものの、そのために基本場の状態が簡単に求まらないという難点もある。また、研究者によって基本場のとり方もまちまちであったりもする。

ここでは熱力学に極力則った形式で、基本場の状態を求めていくことにする。この場合、基本場を規定する以下の方程式系

1.

静水圧の関係式(1.24)

$\displaystyle\frac{\displaystyle d\overline{p}}{\displaystyle dz}=\overline{% \rho}\,\overline{g}$ (1.59)

$\displaystyle\mathrm{or}\quad\frac{\displaystyle d\overline{p}}{\displaystyle dr% }=-\overline{\rho}\,\overline{g}$ (1.52)
2.

断熱的な圧力変化と温度変化の関係(A.16)

$\frac{\displaystyle d\overline{T}}{\displaystyle d\overline{p}}=\frac{% \displaystyle\overline{\alpha}\,\overline{T}}{\displaystyle\overline{\rho}\,% \overline{C_{p}}}$ (1.60)
3.

断熱圧縮率の熱力学的な定義(A.12)

$\frac{\displaystyle 1}{\displaystyle\overline{\rho}}\frac{\displaystyle d% \overline{\rho}}{\displaystyle d\overline{p}}=\overline{\chi_{a}}$ (1.61)
4.

Grüneisen parameter (1.33)

$\overline{\gamma}=\frac{\displaystyle\overline{\alpha}}{\displaystyle\overline% {\rho}\overline{C_{p}}\overline{\chi_{a}}}$ (1.62)

を適当な仮定のもとで積分することにより、基本場を構成することになる。ただし、8個の未知量 ( $\overline{p}$ 、 $\overline{\rho}$ 、 $\overline{g}$ 、 $\overline{T}$ 、 $\overline{\alpha}$ 、 $\overline{C_{p}}$ 、 $\overline{\chi_{a}}$ 、 $\overline{\gamma}$ ) を決定するには、上の4式の他に4 つの条件を指定する必要がある。

デカルト座標系の場合によく用いられるもの

1つの簡単な例は、 $\overline{g}$ 、 $\overline{C_{p}}$ 、 $\overline{\alpha}$ 、 $\overline{\gamma}$ を一定と仮定してしまうことにより得られる。まず式(1.62)、(1.59)、(1.61)から Adams-Willamson の式

\frac{\displaystyle 1}{\displaystyle\overline{\rho}}\frac{\displaystyle d% \overline{\rho}}{\displaystyle dz}=\overline{\rho}\,\overline{g}\,\overline{% \chi_{a}}=\frac{\displaystyle\overline{g}\,\overline{\alpha}}{\displaystyle% \overline{C_{p}}\,\overline{\gamma}}

(1.63)

が導かれる。仮定により式(1.63)の右辺は定数なので、解析的に積分してやると

\overline{\rho}(z)=\overline{\rho}(z=0)\exp\left[\frac{\displaystyle\overline{% g}\,\overline{\alpha}}{\displaystyle\overline{C_{p}}\,\overline{\gamma}}z% \right]=\overline{\rho}(z=0)\exp\left[\frac{\displaystyle z}{\displaystyle% \overline{h_{d}}}\right]

(1.64)

を得る。ここで $\overline{h_{d}}$ は式(1.31)で定義した、密度変化のスケールハイトである。また $z$ を対流層の厚さ $b$ で無次元化してやると、

\overline{\rho}(z)=\overline{\rho}(z=0)\exp\left[\frac{\displaystyle z}{% \displaystyle b}\frac{\displaystyle b}{\displaystyle\overline{h_{d}}}\right]=% \overline{\rho}(z=0)\exp\left[\frac{\displaystyle z}{\displaystyle b}\frac{% \displaystyle\overline{D}}{\displaystyle\overline{\gamma}}\right]

(1.65)

となる。ここで

\overline{D}=\frac{\displaystyle\overline{\alpha}\,\overline{g}\,b}{% \displaystyle\overline{C_{p}}}

(1.66)

は基本場の dissipation number (式(1.35)を見よ) である。式(1.64)で得られた $\overline{\rho}$ を式(1.59)に代入して積分すると、基本場の圧力分布が

\overline{p}(z)=\overline{\rho}(z=0)\,\overline{g}\,\overline{h_{d}}\left[\exp% \left(\frac{\displaystyle z}{\displaystyle\overline{h_{d}}}\right)-1\right]

(1.67)

と求まる。ただし $\overline{p}(z=0)=0$ とした。基本場の温度分布についても同様である。式(1.59)と(1.60)より

\frac{\displaystyle 1}{\displaystyle\overline{T}}\frac{\displaystyle d% \overline{T}}{\displaystyle dz}=\frac{\displaystyle\overline{\alpha}\,% \overline{g}}{\displaystyle\overline{C_{p}}}

(1.68)

が得られ、さらに積分すると

\overline{T}(z)=\overline{T}(z=0)\exp\left(\frac{\displaystyle\overline{\alpha% }\,\overline{g}}{\displaystyle\overline{C_{p}}}z\right)=\overline{T}(z=0)\exp% \left(\overline{\gamma}\frac{\displaystyle z}{\displaystyle\overline{h_{d}}}% \right)=\overline{T}(z=0)\exp\left(z\frac{\displaystyle\overline{D}}{% \displaystyle b}\right)

(1.69)

となる。圧力変化と密度変化のスケールハイトは $\overline{h_{d}}$ で共通だが、温度変化のスケールハイトは $\overline{h_{d}}/\overline{\gamma}=b/\overline{D}$ である。この基本場の欠点は、深部で対流が起こりにくくなることである。なぜなら、式(1.68)、(1.69)より断熱温度勾配を求めてみると

\left(\frac{\displaystyle d\overline{T}}{\displaystyle dz}\right)_{a}=\frac{% \displaystyle\overline{\alpha}\,\overline{g}}{\displaystyle\overline{C_{p}}}% \overline{T}=\frac{\displaystyle\overline{\alpha}\,\overline{g}\,\overline{T}(% z=0)}{\displaystyle\overline{C_{p}}}\exp\left(\overline{\gamma}\frac{% \displaystyle z}{\displaystyle\overline{h_{d}}}\right)=\left(\frac{% \displaystyle d\overline{T}}{\displaystyle dz}\right)_{a}(z=0)\exp\left(% \overline{\gamma}\frac{\displaystyle z}{\displaystyle\overline{h_{d}}}\right)

(1.70)

即ち、断熱温度勾配が深さとともに指数関数的に増大してしまうことになるからである。

これに対し、Tackley [9] では、上とは異なった方法が用いられている。そこでは $\overline{g}$ 、 $\overline{C_{p}}$ は一定とみなすものの、 $\overline{\alpha}$ と $\overline{\gamma}$ は以下のような関数形で密度に依存して変化すると仮定する。

	$\displaystyle\frac{\displaystyle\alpha}{\displaystyle\alpha_{o}}$	$\displaystyle=\exp\left\{-\frac{\displaystyle{\delta_{T}}_{o}}{\displaystyle% \kappa}\left[1-\left(\frac{\displaystyle\rho_{o}}{\displaystyle\rho}\right)^{% \kappa}\right]\right\}$		(1.71)
	$\displaystyle\frac{\displaystyle\gamma}{\displaystyle\gamma_{o}}$	$\displaystyle=\frac{\displaystyle\rho_{o}}{\displaystyle\rho}$		(1.72)

ここで、式(1.71)は経験的に得られている Anderson-Grüneisen parameter $\delta_{T}$

\delta_{T}\equiv\left(\frac{\displaystyle\partial\ln\alpha}{\displaystyle% \partial\ln\rho}\right)_{T}={\delta_{T}}_{o}\left(\frac{\displaystyle\rho_{o}}% {\displaystyle\rho}\right)^{\kappa}

(1.73)

が断熱線に沿っても成り立つとの仮定による。式(1.73)に現われる $\delta_{T}$ はおよそ $4\sim 6$ 、 $\kappa$ はおよそ $1.4$ 程度の値を持つことが実験的に知られている。また式(1.72)は Mie-Grüneisen の状態方程式からの派生である (おそらく)。以上の条件式を数値的に積分することにより基本場が構成できる。

1.4 相転移の取り扱い

相転移を厳密に熱力学に則って計算するのは繁雑である。ここではマントル対流業界でよく用いられている、拡張された Boussinesq 近似のもとでの phase function に基づく扱いについて紹介する。以下の記述は主に [2] を参考にした。また以下では簡単のため相転移は1つのみと仮定しているが、相転移が複数ある場合も同様な定式化により取り扱いが可能である。

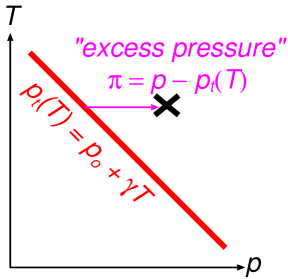
Refer to caption — Figure 1: 仮定している相平衡図、及び相転移の計算に用いる “excess pressure” $\pi$ の定義の概念図。

方程式を簡単化するため、以下では Clapeyron 勾配 $\gamma$ を一定にとり、相転移が起こる圧力 $p_{t}$ を温度 $T$ の関数として

p_{t}(T)=p_{o}+\gamma T

(1.74)

と仮定する。ここで $p_{o}$ は温度 $T=0$ において相転移が起こる圧力である。この値からの圧力のずれによって相転移の起こり方が決まると仮定しよう。そこで以下のように余剰圧力(excess pressure)とでもいうべき量 $\pi$ を定義する。

\pi=p-p_{t}(T)=p-p_{o}-\gamma T

(1.75)

(実際には静水圧を仮定して圧力を深さに読み換える。) さらに、2つの相の分率を表わす phase function $\Gamma$ (ただし $0\leq\Gamma\leq 1$ 、 $\Gamma=0$ で低圧相、 $\Gamma=1$ で高圧相)を $\pi$ の関数として導入する。よく使われる形は

\Gamma(\pi)=\frac{\displaystyle 1}{\displaystyle 2}\left[1+\tanh\left(\frac{% \displaystyle\pi}{\displaystyle\Delta p}\right)\right]

(1.76)

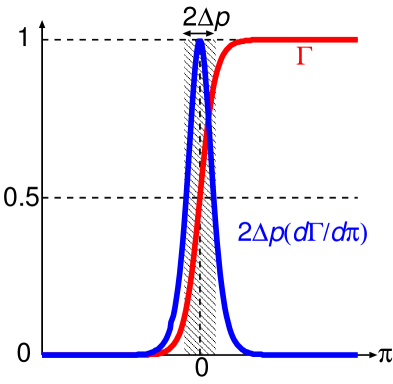
である。ここで、 $\Delta p$ は相転移にかかる圧力の幅に相当するパラメータである。また、式(1.76)を $\pi$ で微分すると、

\frac{\displaystyle d\Gamma}{\displaystyle d\pi}=\frac{\displaystyle 1}{% \displaystyle 2\Delta p}\left[1-\tanh^{2}\left(\frac{\displaystyle\pi}{% \displaystyle\Delta p}\right)\right]=\frac{\displaystyle 2}{\displaystyle% \Delta p}\Gamma(1-\Gamma)

(1.77)

となる。これらのグラフを図2に示す。この関数 $\Gamma$ は相転移を数値的に簡便に取り扱うために恣意的に導入したに過ぎないことに注意しよう。しかも後に見るように、 $\Gamma$ の関数形そのものではなく、その微分 $\frac{\displaystyle d\Gamma}{\displaystyle d\pi}$ のみが意味を持っているので、式 (1.76) を盲目的に信じる必要もない。実際に Honda et al. [4] などでは、 $\frac{\displaystyle d\Gamma}{\displaystyle d\pi}$ を Gaussian と仮定してシミュレーションを行っている。

phase function $\Gamma$ を用いて、マントル対流の基礎方程式に相転移の効果を導入することを考えよう。以下では簡単のため、密度と比エントロピー以外の全ての熱力学的な量は相転移によって不変である(1次の相転移に相当)と仮定する。まず状態方程式を修正しよう。マントル物質の密度は温度 $T$ と圧力 $p$ に加え、phase function $\Gamma$ にも依存する関数で与えられるとしよう。

\rho=\rho(T,p,\Gamma)

1.2章の取り扱いに倣い、密度分布を基本場( $\bar{~{}}$ つき)と基本場からのずれ( $\prime$ つき)の2つに分離すると、

$\displaystyle\rho$	$\displaystyle=\overline{\rho}+\rho\prime=\rho(\overline{T}+T\prime,\overline{p% }+p\prime,\overline{\Gamma}+\Gamma\prime)$
	$\displaystyle\simeq\overline{\rho}(\overline{T},\overline{p},\overline{\Gamma}% )+\overline{\left(\frac{\displaystyle\partial\rho}{\displaystyle\partial p}% \right)_{T,\Gamma}}p\prime+\overline{\left(\frac{\displaystyle\partial\rho}{% \displaystyle\partial T}\right)_{p,\Gamma}}T\prime+\overline{\left(\frac{% \displaystyle\partial\rho}{\displaystyle\partial\Gamma}\right)_{p,T}}\Gamma\prime$
	$\displaystyle=\overline{\rho}(\overline{T},\overline{p},\overline{\Gamma})+% \overline{\rho}\,\overline{\chi}_{T}\,p\prime-\overline{\alpha}\,\overline{% \rho}\,T\prime+\overline{\Delta\rho}\,\Gamma\prime$	(1.78)

ここで、 $\overline{\Delta\rho}\equiv\overline{\rho_{h}}-\overline{\rho_{\ell}}$ は高圧相と低圧相の密度差である。 (今後も同様に、下つき添字_ℓで低圧相、_hで高圧相を示す。) 以下では簡便のため $\frac{\displaystyle\overline{\Delta\rho}}{\displaystyle\overline{\rho}}=\frac{% \displaystyle\Delta\rho}{\displaystyle\rho}$ と書き、これを一定とみなす。式(1.25)に倣ってスケーリングを施すと、

\frac{\displaystyle\rho^{\ast}}{\displaystyle\overline{\rho}^{\ast}}=1+% \overline{\chi}_{T}^{\ast}p\prime^{\ast}M^{2}Pr-\overline{\alpha}^{\ast}T% \prime^{\ast}\epsilon+\Gamma\prime\frac{\displaystyle\Delta\rho}{\displaystyle\rho}

(1.79)

を得る。同様に、エントロピーの変化量(式(1.21))は以下のように修正されるべきであろう。

ds=\frac{\displaystyle C_{p}}{\displaystyle T}dT-\frac{\displaystyle\alpha}{% \displaystyle\rho}dp-\Delta s\,d\Gamma

(1.80)

ここで、 $\Delta s\equiv s_{\ell}-s_{h}$ は低圧相と高圧相の比エントロピーの差である。なお、Clausius-Clapeyron の式(A.24)より、 $\Delta s$ と $\Delta\rho$ の間には

\gamma=\frac{\displaystyle s_{\ell}-s_{h}}{\displaystyle\rho_{\ell}^{-1}-\rho_% {h}^{-1}}=\rho_{\ell}\rho_{h}\frac{\displaystyle s_{\ell}-s_{h}}{\displaystyle% \rho_{h}-\rho_{\ell}}=\rho_{\ell}\rho_{h}\frac{\displaystyle\Delta s}{% \displaystyle\Delta\rho}

(1.81)

なる関係がある。これを用いれば式(1.80)は、

ds=\frac{\displaystyle C_{p}}{\displaystyle T}dT-\frac{\displaystyle\alpha}{% \displaystyle\rho}dp-\frac{\displaystyle\gamma\Delta\rho}{\displaystyle\rho^{2% }}d\Gamma

(1.82)

とも表わすことができる (ここで $\rho_{\ell}\rho_{h}\simeq\rho^{2}$ と近似した)。

これらを用いて、拡張されたBoussinesq近似のもとでの基礎方程式を修正してみよう。この場合、質量保存則はBoussinesq近似と同じ非圧縮の仮定(式(1.29)) を用いてよい。以下では Navier-Stokes方程式と熱エネルギーの保存則がどのように修正されるべきかを論じる。相転移による密度変化の影響を考慮すると、スケーリングされた非弾性近似のもとでの Navier-Stokes 方程式は

\displaystyle 0=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}\overline{% \chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle D}{\displaystyle\gamma_{r}}% \frac{\displaystyle{C_{p}}_{r}}{\displaystyle{C_{v}}_{r}}-\overline{\rho}^{% \ast}\overline{\alpha}^{\ast}\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra+% \overline{\rho}^{\ast}\overline{g}_{i}^{\ast}\Gamma\prime\,Rb+\frac{% \displaystyle\partial}{\displaystyle\partial x_{j}^{\ast}}\left[\mu^{\ast}% \left(\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle\partial x_{j}^{% \ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{\displaystyle\partial x_{i}^{% \ast}}-\frac{\displaystyle 2}{\displaystyle 3}\frac{\displaystyle\partial v_{k% }^{\ast}}{\displaystyle\partial x_{k}^{\ast}}\delta_{ij}\right)\right]

(1.83)

と書ける。ここで新たな無次元量 $R b$ を

Rb\equiv\frac{\displaystyle b^{3}\rho_{r}^{2}{C_{p}}_{r}g_{r}}{\displaystyle% \mu_{r}k_{r}}\frac{\displaystyle\Delta\rho}{\displaystyle\rho}

(1.84)

と置いた。これは相転移による密度変化が対流を促進(または抑制)する効果の強さを表わす量で、phase boundary Rayleigh 数と呼ばれることもある。さらに Boussinesq 近似を施すと、

\displaystyle 0=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\overline{\rho}^{\ast}\overline{\alpha}^{\ast}\overline% {g}_{i}^{\ast}T\prime^{\ast}\,Ra+\overline{\rho}^{\ast}\overline{g}_{i}^{\ast}% \Gamma\prime\,Rb+\frac{\displaystyle\partial}{\displaystyle\partial x_{j}^{% \ast}}\left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{% \displaystyle\partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{% \displaystyle\partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}% \frac{\displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}% \delta_{ij}\right)\right]

(1.85)

を得る。これと式(1.37)と比較すると、温度変化による密度変化に加え、相転移による密度変化が浮力に寄与していることが分かる。

次に、熱エネルギーの保存則を修正する。式(1.82)を式(1.16)に代入すると、

\rho C_{p}\frac{\displaystyle DT}{\displaystyle Dt}-\alpha T\frac{% \displaystyle Dp}{\displaystyle Dt}-T\gamma\frac{\displaystyle\Delta\rho}{% \displaystyle\rho}\frac{\displaystyle D\Gamma}{\displaystyle Dt}=\frac{% \displaystyle\partial}{\displaystyle\partial x_{i}}\left(k\frac{\displaystyle% \partial T}{\displaystyle\partial x_{i}}\right)+\Phi+\rho H

(1.86)

となる。左辺第3項が相転移によって新たにつけ加わった項であり、これは相転移によるエントロピー変化の効果を表わしている。次にこの式のスケーリングを試みる。左辺第1項、第2項、及び右辺は式(1.41)などと同じなので省略し、式 (1.41)の導出にならって左辺第3項のスケーリングを考えると、

	$\displaystyle-T\gamma\frac{\displaystyle\Delta\rho}{\displaystyle\rho}\frac{% \displaystyle D\Gamma}{\displaystyle Dt}$	$\displaystyle\Rightarrow-\Delta T_{r}\left(\overline{T}^{\ast}+T\prime^{\ast}% \right)\frac{\displaystyle\rho_{r}g_{r}b}{\displaystyle\Delta T_{r}}\gamma^{% \ast}\frac{\displaystyle\Delta\rho}{\displaystyle\rho}\frac{\displaystyle k_{r% }}{\displaystyle b^{2}\rho_{r}{C_{p}}_{r}}\frac{\displaystyle D\Gamma}{% \displaystyle Dt^{\ast}}$
		$\displaystyle=-\frac{\displaystyle k_{r}\Delta T_{r}}{\displaystyle b^{2}}% \underbrace{\frac{\displaystyle g_{r}b}{\displaystyle{C_{p}}_{r}\Delta T_{r}}% \frac{\displaystyle\Delta\rho}{\displaystyle\rho}}_{=D\frac{\displaystyle Rb}{% \displaystyle Ra}}\gamma^{\ast}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)% \frac{\displaystyle D\Gamma}{\displaystyle Dt^{\ast}}$		(1.87)

ここで、Clapeyron 勾配 $\gamma$ に含まれる圧力は静水圧 $\rho_{r}g_{r}b$ によりスケーリングした。これより、非弾性近似のもとでのスケーリングされた熱エネルギーの保存則は、

	$\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle D% }{\displaystyle Dt^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)-D% \overline{\alpha}^{\ast}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)% \overline{\rho}^{\ast}\overline{g}_{i}^{\ast}v_{i}^{\ast}-D\frac{\displaystyle Rb% }{\displaystyle Ra}\gamma^{\ast}\left(\overline{T}^{\ast}+T\prime^{\ast}\right% )\frac{\displaystyle D\Gamma}{\displaystyle Dt^{\ast}}$
	$\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[k^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]+\Phi^{\ast}\frac{% \displaystyle D}{\displaystyle Ra}+\overline{\rho}^{\ast}H^{\ast}\left(\frac{% \displaystyle b^{2}H_{r}\rho_{r}}{\displaystyle k_{r}\Delta T_{r}}\right)$		(1.88)

相転移の効果は左辺第3項に含まれている。この項は Dissipation number $D$ でスケーリングされていることに注意しよう。これより、 $D\rightarrow 0$ の極限では熱輸送に相転移の効果は現われないことが分かる ¹¹ 1 この議論から、Boussinesq 近似のもとでは相転移の潜熱の効果を無視することが多い。ただし、Ogawa and Nakamura [5] によれば、固相-液相の相転移では Boussinesq 近似であっても潜熱の効果は必ずしも無視すべきではないと指摘されている。。

これまでに議論した基礎方程式の導出は、phase function $\Gamma$ の具体的な関数形にはよらないものであった。また式(1.88)には $\Gamma$ の Lagrange 微分が含まれているので、解くのが少々面倒である。そこで、式(1.75)及び(1.76)を用いてこれらの式をより簡便な形に書き直してみる。式(1.75)内の余剰圧力を静水圧 $\rho_{r}g_{r}b$ でスケーリングすると、

\pi^{\ast}=\underbrace{\frac{\displaystyle 1}{\displaystyle\rho_{r}g_{r}b}% \frac{\displaystyle\mu_{r}k_{r}}{\displaystyle b^{2}\rho_{r}{C_{p}}_{r}}}_{=% \frac{\displaystyle\epsilon}{\displaystyle Ra}}\left(p^{\ast}-p_{t}^{\ast}% \right)-\gamma^{\ast}T^{\ast}

ここで、 $\frac{\displaystyle\epsilon}{\displaystyle Ra}$ なる因子は圧力のスケーリングに用いた基準値の違いに起因している。これを用いると、phase function $\Gamma$ の微小変化は

\delta\Gamma=\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\delta\pi^% {\ast}=\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\left(\frac{% \displaystyle\epsilon}{\displaystyle Ra}\delta p^{\ast}-\gamma^{\ast}\delta T^% {\ast}\right)

と与えられる。これをNavier-Stokes方程式(1.83)に代入、整理すると、

	$\displaystyle 0=-\frac{\displaystyle\partial p\prime^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}+\overline{g}_{i}^{\ast}\overline{\rho}^{\ast}\overline{% \chi}_{T}^{\ast}p\prime^{\ast}\frac{\displaystyle D}{\displaystyle\gamma_{r}}% \frac{\displaystyle{C_{p}}_{r}}{\displaystyle{C_{v}}_{r}}-\overline{\rho}^{% \ast}\overline{g}_{i}^{\ast}T\prime^{\ast}\,Ra\left(\overline{\alpha}^{\ast}+% \gamma^{\ast}\frac{\displaystyle Rb}{\displaystyle Ra}\frac{\displaystyle d% \Gamma}{\displaystyle d\pi^{\ast}}\right)$
	$\displaystyle+\frac{\displaystyle\partial}{\displaystyle\partial x_{j}^{\ast}}% \left[\mu^{\ast}\left(\frac{\displaystyle\partial v_{i}^{\ast}}{\displaystyle% \partial x_{j}^{\ast}}+\frac{\displaystyle\partial v_{j}^{\ast}}{\displaystyle% \partial x_{i}^{\ast}}-\frac{\displaystyle 2}{\displaystyle 3}\frac{% \displaystyle\partial v_{k}^{\ast}}{\displaystyle\partial x_{k}^{\ast}}\delta_% {ij}\right)\right]$		(1.89)

を得る。これと式(1.38)を比較すると、相転移による密度変化の影響は、実効的な熱膨張率を

\alpha^{\ast}_{e\!f\!f}\equiv\overline{\alpha}^{\ast}+\gamma^{\ast}\frac{% \displaystyle Rb}{\displaystyle Ra}\frac{\displaystyle d\Gamma}{\displaystyle d% \pi^{\ast}}=\overline{\alpha}^{\ast}+P\frac{\displaystyle d\Gamma}{% \displaystyle d\pi^{\ast}}

(1.90)

の如く定義し直したことと同じである。ここで新たな無次元量 $P$ を

P\equiv\gamma^{\ast}\frac{\displaystyle Rb}{\displaystyle Ra}

(1.91)

と置いた。これは時に phase buoyancy parameter とも呼ばれる。熱輸送方程式(1.88)の左辺第3項も同様に変形しよう。

	$\displaystyle\frac{\displaystyle D\Gamma}{\displaystyle Dt^{\ast}}$	$\displaystyle=\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\frac{% \displaystyle D\pi^{\ast}}{\displaystyle Dt^{\ast}}=\frac{\displaystyle d% \Gamma}{\displaystyle d\pi^{\ast}}\left[\frac{\displaystyle\epsilon}{% \displaystyle Ra}\frac{\displaystyle Dp^{\ast}}{\displaystyle Dt^{\ast}}-% \gamma^{\ast}\frac{\displaystyle DT^{\ast}}{\displaystyle Dt^{\ast}}\right]=% \frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\left[\underbrace{\frac% {\displaystyle\epsilon}{\displaystyle Ra}\frac{\displaystyle D\overline{p}^{% \ast}}{\displaystyle Dt^{\ast}}}_{=\overline{\rho}^{\ast}\overline{g}_{i}^{% \ast}v_{i}^{\ast}}+\underbrace{\frac{\displaystyle\epsilon}{\displaystyle Ra}% \frac{\displaystyle Dp\prime^{\ast}}{\displaystyle Dt^{\ast}}}_{=0}-\gamma^{% \ast}\frac{\displaystyle D}{\displaystyle Dt^{\ast}}\left(\overline{T}^{\ast}+% T\prime^{\ast}\right)\right]$
		$\displaystyle=\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\left[% \overline{\rho}^{\ast}\overline{g}_{i}^{\ast}v_{i}^{\ast}-\gamma^{\ast}\frac{% \displaystyle D}{\displaystyle Dt^{\ast}}\left(\overline{T}^{\ast}+T\prime^{% \ast}\right)\right]$		(1.92)

これを(1.88)に代入して整理すると、

	$\displaystyle\left[\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}+D\frac{% \displaystyle Rb}{\displaystyle Ra}{\gamma^{\ast}}^{2}\left(\overline{T}^{\ast% }+T\prime^{\ast}\right)\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}% \right]\frac{\displaystyle D}{\displaystyle Dt^{\ast}}\left(\overline{T}^{\ast% }+T\prime^{\ast}\right)-D\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\left(% \overline{\alpha}^{\ast}+\gamma^{\ast}\frac{\displaystyle Rb}{\displaystyle Ra% }\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}\right)\overline{\rho}% ^{\ast}\overline{g}_{i}^{\ast}v_{i}^{\ast}$
	$\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[k^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]+\Phi^{\ast}\frac{% \displaystyle D}{\displaystyle Ra}+\overline{\rho}^{\ast}H^{\ast}\left(\frac{% \displaystyle b^{2}H_{r}\rho_{r}}{\displaystyle k_{r}\Delta T_{r}}\right)$		(1.93)

を得る。これと式(1.42)を比較すると、相転移によるエントロピーの出入りは、式(1.90)で与えられる実効的な熱膨張率に加え、実効的な熱容量を

\left(\rho C_{p}\right)_{e\!f\!f}\equiv\overline{\rho}^{\ast}\overline{C_{p}}^% {\ast}+D\frac{\displaystyle Rb}{\displaystyle Ra}{\gamma^{\ast}}^{2}\left(% \overline{T}^{\ast}+T\prime^{\ast}\right)\frac{\displaystyle d\Gamma}{% \displaystyle d\pi^{\ast}}

(1.94)

の如く定義し直したことと同じであることが分かる。

式(1.89)及び(1.93) をまとめると、相転移の効果は以下の3つに分かれていることが理解できる。

1.

温度の違いによる相転移境界のずれ。これは式(1.89)の右辺第3項の、相転移による浮力の変化として現われる。
2.

潜熱の出入りによる温度変化。これは式(1.93)の左辺第2項の、相転移による断熱温度勾配の変化として現われる。
3.

潜熱の出入りによる温度変化が原因となる相転移境界のずれ。これは式(1.93)の左辺第2項の、相転移による熱容量の変化として現われる。

ただし Boussinesq 近似を扱う場合には潜熱の出入りは無視されるので、上記の (2)及び(3)の効果は含まれない。また、(3)の効果を残すと式(1.93)が温度に関して非線型になってしまうため、この効果は多くの場合は無視されている。とはいえ無次元化された Clapeyon 勾配の値は通常小さいので、 ${\gamma^{\ast}}^{2}$ を含む項を落とすことによる悪影響は小さいと期待される。

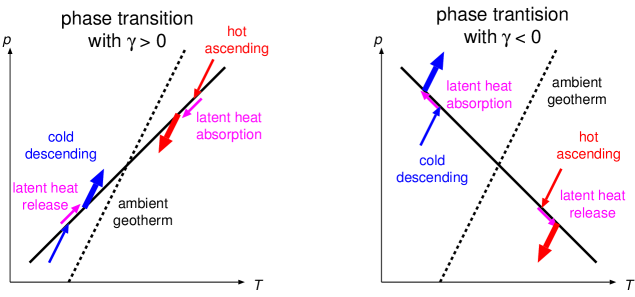
上記の(1)と(2)の効果が対流に及ぼす影響を図3に概念的に示す。一例として低温の下降流の挙動にのみ注目して考える。まず(1)温度の違いによる相転移境界のずれの効果のみを考えよう。 $\gamma>0$ の場合、低温の下降流は周囲より浅い部分で高密度の相へ転移する。即ち、より大きな負の浮力を獲得することができる。逆に $\gamma<0$ の場合には下降流は周囲より深部で高密度の相へ転移するため、負の浮力を獲得できない。これより(1)の効果では、 $\gamma>0$ の相転移はこれを横切る流れを加速し、その反対に $\gamma<0$ の相転移は阻害する方向に働く。一方、(2)潜熱の出入りによる温度変化は(1)と正反対の効果を持つ。低温の下降流が $\gamma>0$ の相転移を通過する際に潜熱が解放される。即ち下降流内の温度が上がり、熱的な負の浮力が小さくなる。逆に $\gamma<0$ の相転移を通過する際には潜熱が吸収され、下降流内の温度が下がり、熱的な負の浮力が大きくなる。これより(2)の効果では、 $\gamma>0$ の相転移はこれを横切る流れを阻害し、その反対に $\gamma<0$ の相転移は加速する方向に働く。ちなみに(3)の効果は、 $\gamma$ の符号によらず、相転移を横切る流れを阻害する方向に働く。

また、さらなる簡略化として、相転移面の起こる位置の温度変化を無視するという近似もある。この場合、 $\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}$ の計算において温度 $T$ を一定とみなし、これを深さのみの関数と仮定する。さらに、この $\frac{\displaystyle d\Gamma}{\displaystyle d\pi^{\ast}}$ をもとにして得られた $\alpha_{e\!f\!f}$ を用いて、相転移における密度変化の影響を取り入れる。この近似では、温度分布が変化しても相転移面の位置を不変に保つことができることに加え、相転移による対流の層構造の有無に関してよい近似となっている [2] ので、計算の簡略化としてよく用いられている (例えば [4, 7]など)。

	$\displaystyle\overline{\rho}^{\ast}\overline{C_{p}}^{\ast}\frac{\displaystyle DT% \prime^{\ast}}{\displaystyle Dt^{\ast}}-\overline{\alpha}^{\ast}T\prime^{\ast}% \overline{g}_{i}^{\ast}v_{i}^{\ast}\overline{\rho}^{\ast}D$	$\displaystyle=\frac{\displaystyle\partial}{\displaystyle\partial x_{i}^{\ast}}% \left[\overline{k}^{\ast}\frac{\displaystyle\partial}{\displaystyle\partial x_% {i}^{\ast}}\left(\overline{T}^{\ast}+T\prime^{\ast}\right)\right]$
		$\displaystyle+\Phi^{\ast}\frac{\displaystyle D}{\displaystyle Ra}+\overline{% \rho}^{\ast}H^{\ast}\left(\frac{\displaystyle b^{2}H_{r}\rho_{r}}{% \displaystyle k_{r}\Delta T_{r}}\right)$		(1.44)

	$\displaystyle\frac{\displaystyle d\overline{p}}{\displaystyle dz}=\overline{% \rho}\,\overline{g}$		(1.59)
	$\displaystyle\mathrm{or}\quad\frac{\displaystyle d\overline{p}}{\displaystyle dr% }=-\overline{\rho}\,\overline{g}$		(1.52)