Appendix F 重力・ジオイド

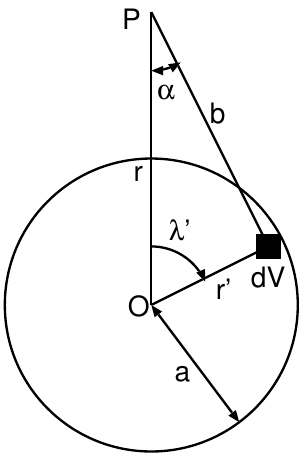
図のように、半径が$a$の球体をとり、球の内部の微小体積素片$dV$が点Pに及ぼ す万有引力を考える。 その加速度を$d{g}_m$ と書くと、

$$d{g}_m=\frac{G\rho (r^{\prime })dV}{b^2}$$

である。 これを積分することで、この球全体がPに及ぼす万有引力$g_m$を求めることがで きる。 系の対称性より、Pから球の中心Oに向かう成分のみを考えれば十分であるから、

	$g_m={\displaystyle \int 𝑑g_m\cos \alpha }$	$=G{\displaystyle \int \frac{\rho (r^{\prime })\cos \alpha }{b^2}𝑑V}$		(F.1)
		$=G{\displaystyle {\int }_0^a}{\displaystyle {\int }_0^{\pi }}{\displaystyle {\int }_0^{2\pi }}{\displaystyle \frac{\rho (r^{\prime })r^{\prime }{}^2\sin {\lambda }^{\prime }\cos \alpha }{b^2}}𝑑{\psi }^{\prime }𝑑{\lambda }^{\prime }𝑑r^{\prime }$		(F.2)

と表される。

この積分を実行するために、${\lambda }^{\prime }$ と $\alpha$ を消去することを考える。 余弦定理より

$$\cos \alpha =\frac{r^2+b^2-r^{\prime }{}^2}{2rb}$$

(F.3)

が成り立つ。 同様に

$$b^2=r^2+r^{\prime }{}^2-2r{r}^{\prime }\cos {\lambda }^{\prime }$$

(F.4)

もいえる。 式(F.4)の両辺を${\lambda }^{\prime }$で微分することにより、

$$\sin {\lambda }^{\prime }d{\lambda }^{\prime }=\frac{b}{r{r}^{\prime }}db$$

(F.5)

が成り立つことも確認できる。 ただしこの際、$r$と$r^{\prime }$は一定としてある。 また $0\le {\lambda }^{\prime }\le \pi$ であることから、$|r-r^{\prime }|\le b\le r+r^{\prime }$ である。 点Pが球の内側にあるか外側にあるかによって、積分範囲が変わることに注意。

式(F.3)と(F.5)を式(F.2)に代入して整理すると、

	$g_m$	$=G{\displaystyle {\int }_0^a}{\displaystyle {\int }_0^{2\pi }}{\displaystyle {\int }_{|r-r^{\prime }|}^{r+r^{\prime }}}{\displaystyle \frac{\rho (r^{\prime })r^{\prime }{}^2}{b^2}}{\displaystyle \frac{r^2+b^2-r^{\prime }{}^2}{2rb}}{\displaystyle \frac{b}{r{r}^{\prime }}}𝑑b𝑑{\psi }^{\prime }𝑑r^{\prime }$
		$={\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_0^a}{\displaystyle {\int }_{|r-r^{\prime }|}^{r+r^{\prime }}}\rho (r^{\prime })r^{\prime }\left({\displaystyle \frac{r^2-r^{\prime }{}^2}{b^2}}+1\right)𝑑b𝑑r^{\prime }$
		$={\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_0^a}\rho (r^{\prime })r^{\prime }{\left[-{\displaystyle \frac{r^2-r^{\prime }{}^2}{b}}+b\right]}_{|r-r^{\prime }|}^{r+r^{\prime }}𝑑r^{\prime }$		(F.6)

を得る。 以下、$r$と$a$ の大小関係によって場合分けを行う。

• •

  $r\ge a$ (点Pが球の表面または外側にある) 場合には、式 (F.6)中の$r-r^{\prime }$は常に非負である。 よって、

  	$g_m$	$={\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_0^a}\rho (r^{\prime })r^{\prime }{\left[-{\displaystyle \frac{r^2-r^{\prime }{}^2}{b}}+b\right]}_{r-r^{\prime }}^{r+r^{\prime }}𝑑r^{\prime }$
  		$={\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_0^a}\rho (r^{\prime })r^{\prime }(4r^{\prime })𝑑r^{\prime }={\displaystyle \frac{4\pi G}{r^2}}{\displaystyle {\int }_0^a}\rho (r^{\prime })r^{\prime }{}^2𝑑r^{\prime }$		(F.7)

  となる。 ここで、球の全質量$M$が

  $$M=4\pi {\int }_0^a\rho (r^{\prime })r^{\prime }{}^2𝑑r^{\prime }$$

  (F.8)

  であることを用いると結局、

  $$g_m=\frac{GM}{r^2}$$

  (F.9)

  を得る。 即ち、球対称な密度分布をもつ物体の外側における万有引力による加速 度は、球の中心に全質量が集中していると考えた場合に得られるものと 同じである。

• •

  (点Pが球の内側にある) 場合には、$r-r^{\prime }$の符号によって場 合分けが必要である。

  	$g_m$	$={\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_0^r}\rho (r^{\prime })r^{\prime }{\left[-{\displaystyle \frac{r^2-r^{\prime }{}^2}{b}}+b\right]}_{r-r^{\prime }}^{r+r^{\prime }}𝑑r^{\prime }+{\displaystyle \frac{\pi G}{r^2}}{\displaystyle {\int }_r^a}\rho (r^{\prime })r^{\prime }{\left[-{\displaystyle \frac{r^2-r^{\prime }{}^2}{b}}+b\right]}_{r^{\prime }-r}^{r^{\prime }+r}𝑑r^{\prime }$
  		$={\displaystyle \frac{4\pi G}{r^2}}{\displaystyle {\int }_0^r}\rho (r^{\prime })r^{\prime }{}^2𝑑r^{\prime }$		(F.10)

  右辺第2項の$b$に関する積分は$0$になることに注意。 即ち、$r^{\prime }>r$ にある体積素片からの寄与はなくなり、$0\le r^{\prime }\le r$ の範囲にある体積素片からの寄与のみが残ることになる。

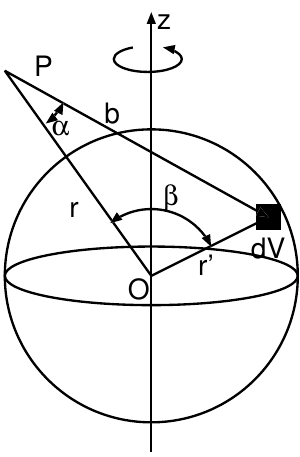
地球のように、自転の効果を受けて扁平になった物体が、物体の外部につくる万 有引力を考える。 この場合も (自転軸に関する対称性を後に仮定するため?)、物体の重心Oに向か う万有引力の成分のみを考えればよい。

$g_m=G{\displaystyle \int \frac{\rho \cos \alpha }{b^2}𝑑V}={\displaystyle \frac{G}{2r^2}}{\displaystyle \int \frac{r}{b}\left[1+\frac{r^2}{b^2}\left(1-\frac{r^{\prime }{}^2}{r^2}\right)\right]\rho 𝑑V}$

(F.11)

この積分を実行するために、$b$ を消去することを考える。 余弦定理より、

$$b^2=r^2+r^{\prime }{}^2-2r{r}^{\prime }\cos \beta$$

(F.12)

であるから、

$$\frac{r}{b}={\left[1+\frac{r^{\prime }{}^2}{r^2}-\frac{2r^{\prime }}{r}\cos \beta \right]}^{-1/2}$$

(F.13)

を得る。 これを式(F.11)に代入すると、

$g_m={\displaystyle \frac{G}{2r^2}}{\displaystyle \int {\left[1+\frac{r^{\prime }{}^2}{r^2}-\frac{2r^{\prime }}{r}\cos \beta \right]}^{-1/2}\left\{1+\left(1-\frac{r^{\prime }{}^2}{r^2}\right){\left[1+\frac{r^{\prime }{}^2}{r^2}-\frac{2r^{\prime }}{r}\cos \beta \right]}^{-1}\right\}\rho 𝑑V}$

(F.14)

となる。

この式を厳密に解析的に積分するのは不可能なので、近似的な方法を考える。 具体的には、式(F.14)を$(r^{\prime }/r)$ のベキに展開し、2次の項までのみを残 すことにする。 即ち、

	${\left[1+{\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right]}^{-1/2}$	$\approx 1-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right)+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right)}^2+\mathrm{\cdots }$
		$\approx 1+{\displaystyle \frac{r^{\prime }}{r}}\cos \beta +{\displaystyle \frac{1}{2}}{\displaystyle \frac{r^{\prime }{}^2}{r^2}}\left(3{\cos }^2\beta -1\right)+\mathrm{\cdots }$
	${\left[1+{\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right]}^{-1}$	$\approx 1-\left({\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right)+{\left({\displaystyle \frac{r^{\prime }{}^2}{r^2}}-{\displaystyle \frac{2r^{\prime }}{r}}\cos \beta \right)}^2+\mathrm{\cdots }$
		$\approx 1+2{\displaystyle \frac{r^{\prime }}{r}}\cos \beta +{\displaystyle \frac{r^{\prime }{}^2}{r^2}}\left(4{\cos }^2\beta -1\right)+\mathrm{\cdots }$

と近似する。 ただしに関する以下のベキ級数展開の表式を繰り返し用いた。

	${(1+\epsilon )}^{-1/2}\approx$	$1-{\displaystyle \frac{\epsilon }{2}}+{\displaystyle \frac{3{\epsilon }^2}{8}}+\mathrm{\cdots }$		(F.15)
	${(1+\epsilon )}^{-1}\approx$	$1-\epsilon +{\epsilon }^2+\mathrm{\cdots }$		(F.16)

これより、

	$g_m$	$\approx {\displaystyle \frac{G}{2r^2}}{\displaystyle \int \left[1+\frac{r^{\prime }}{r}\cos \beta +\frac{1}{2}\frac{r^{\prime }{}^2}{r^2}\left(3{\cos }^2\beta -1\right)+\mathrm{\cdots }\right]}$
		$\times \left\{1+\left(1-{\displaystyle \frac{r^{\prime }{}^2}{r^2}}\right)\left[1+2{\displaystyle \frac{r^{\prime }}{r}}\cos \beta +{\displaystyle \frac{r^{\prime }{}^2}{r^2}}\left(4{\cos }^2\beta -1\right)+\mathrm{\cdots }\right]\right\}\rho dV$
		$\approx {\displaystyle \frac{G}{r^2}}{\displaystyle \int \left[1+\frac{r^{\prime }}{r}\cos \beta +\frac{1}{2}\frac{r^{\prime }{}^2}{r^2}\left(3{\cos }^2\beta -1\right)+\mathrm{\cdots }\right]\left\{1+\frac{r^{\prime }}{r}\cos \beta +\frac{r^{\prime }{}^2}{r^2}\left(2{\cos }^2\beta -1\right)+\mathrm{\cdots }\right\}\rho 𝑑V}$
		$\approx {\displaystyle \frac{G}{r^2}}{\displaystyle \int \left\{1+2\frac{r^{\prime }}{r}\cos \beta +3\frac{r^{\prime }{}^2}{r^2}\left(1-\frac{3}{2}{\sin }^2\beta \right)\right\}\rho 𝑑V}$		(F.17)

を得る。 さらに変形すると

$$g_m=\frac{G}{r^2}\int \rho 𝑑V+2\frac{G}{r^3}\int r^{\prime }\cos \beta \rho dV+3\frac{G}{r^4}\int r^{\prime }{}^2\left(1-\frac{3}{2}{\sin }^2\beta \right)\rho 𝑑V$$

となるが、右辺第1項の積分のうち $\int \rho 𝑑V=M$であり、また第2項の積分 のうち $\int r^{\prime }\cos \beta \rho dV$ は座標原点を重心にとってあることから0とな る。 それゆえ結局、

$$g_m=\frac{GM}{r^2}+3\frac{G}{r^4}\int r^{\prime }{}^2\left(1-\frac{3}{2}{\sin }^2\beta \right)\rho 𝑑V$$

(F.18)

を得る。

ところで式(F.18)の右辺第2項の積分は

$$\int r^{\prime }{}^2\left(1-\frac{3}{2}{\sin }^2\beta \right)\rho 𝑑V=-\frac{1}{2}\int r^{\prime }{}^2\rho 𝑑V+\frac{3}{2}\int r^{\prime }{}^2{\cos }^2\beta \rho dV$$

のように書き直せる。 これを、軸対称な物体の慣性モーメントで表すことを考えよう。 自転軸($z$軸)まわりの慣性モーメントを$C$と書くと、

$C\equiv {\displaystyle \int (x^{\prime }{}^2+y^{\prime }{}^2)\rho 𝑑V}={\displaystyle \int r^{\prime }{}^2{\sin }^2{\lambda }^{\prime }\rho dV}$

(F.19)

となる。 同様に$x$軸まわり及び$y$軸まわりの慣性モーメントをそれぞれ$A$及び$B$と書 くと、

	$A$	$\equiv {\displaystyle \int (y^{\prime }{}^2+z^{\prime }{}^2)\rho 𝑑V}={\displaystyle \int r^{\prime }{}^2({\sin }^2{\lambda }^{\prime }{\sin }^2{\psi }^{\prime }+{\cos }^2{\lambda }^{\prime })\rho 𝑑V}$		(F.20)
	$B$	$\equiv {\displaystyle \int (x^{\prime }{}^2+z^{\prime }{}^2)\rho 𝑑V}={\displaystyle \int r^{\prime }{}^2({\sin }^2\lambda {\cos }^2{\psi }^{\prime }+{\cos }^2{\lambda }^{\prime })\rho 𝑑V}$		(F.21)

であるが、$z$軸まわりの対称性を仮定して$A=B$とみなす。 また式 (F.19)、(F.20)、(F.21)の辺々を加えると、

$$A+B+C=2\int (x^{\prime }{}^2+y^{\prime }{}^2+z^{\prime }{}^2)\rho 𝑑V=2\int r^{\prime }{}^2\rho 𝑑V$$

となるから

${\displaystyle \int r^{\prime }{}^2\rho 𝑑V}={\displaystyle \frac{A+B+C}{2}}=A+{\displaystyle \frac{C}{2}}$

(F.22)

と書ける。 さらに点Pの緯度 (直線OPが$xy$平面となす角) を$\varphi$とし、その位置を

$$(x,y,z)=(r\cos \varphi \cos \psi ,r\cos \varphi \sin \psi ,r\sin \varphi )$$

と書くことにすれば、OP方向の単位ベクトル (ただし外向きを正にとる) は

$$\frac{\overrightarrow{OP}}{|OP|}=(\cos \varphi \cos \psi ,\cos \varphi \sin \psi ,\sin \varphi )$$

と表わされる。 この単位ベクトルと、重心Oと体積要素の位置を結ぶベクトルとの内積を求めて みると、

	$r^{\prime }\cos \beta$	$=(x^{\prime },y^{\prime },z^{\prime })\cdot (\cos \varphi \cos \psi ,\cos \varphi \sin \psi ,\sin \varphi )$
		$=x^{\prime }\cos \varphi \cos \psi +y^{\prime }\cos \varphi \sin \psi +z^{\prime }\sin \varphi$		(F.23)

となる。 これより、

	${\displaystyle \int r^{\prime }{}^2{\cos }^2\beta \rho dV}$	$={\cos }^2\varphi {\cos }^2\psi {\displaystyle \int x^{\prime }{}^2\rho 𝑑V}+{\cos }^2\varphi {\sin }^2\psi {\displaystyle \int y^{\prime }{}^2\rho 𝑑V}+{\sin }^2\varphi {\displaystyle \int z^{\prime }{}^2\rho 𝑑V}$
		$+2{\cos }^2\varphi \sin \psi \cos \psi {\displaystyle \int x^{\prime }{y}^{\prime }\rho 𝑑V}+2\sin \varphi \cos \varphi \sin \psi {\displaystyle \int y^{\prime }{z}^{\prime }\rho 𝑑V}+2\sin \varphi \cos \varphi \cos \psi {\displaystyle \int x^{\prime }{z}^{\prime }\rho 𝑑V}$		(F.24)

となるが、軸対称性の仮定より、

	${\displaystyle \int x^{\prime }{}^2\rho 𝑑V}$	$={\displaystyle \int y^{\prime }{}^2\rho 𝑑V}$		(F.25)
		$={\displaystyle \frac{1}{2}}{\displaystyle \int (x^{\prime }{}^2+y^{\prime }{}^2)\rho 𝑑V}={\displaystyle \frac{C}{2}}$		(F.26)

であり、かつ

	${\displaystyle \int z^{\prime }{}^2\rho 𝑑V}$	$={\displaystyle \int [r^{\prime }{}^2-(x^{\prime }{}^2+y^{\prime }{}^2)]\rho 𝑑V}$
		$=\left(A+{\displaystyle \frac{C}{2}}\right)-C=A-{\displaystyle \frac{C}{2}}$		(F.27)

となる。 さらに $\int x^{\prime }{y}^{\prime }\rho 𝑑V$、$\int y^{\prime }{z}^{\prime }\rho 𝑑V$、 $\int x^{\prime }{z}^{\prime }\rho 𝑑V$ の項 (慣性プロダクトとも呼ばれる) は、座標軸を慣 性主軸にとってあれば0になる。 よって、

${\displaystyle \int r^{\prime }{}^2{\cos }^2\beta \rho dV}={\displaystyle \frac{C}{2}}{\cos }^2\varphi +\left(A-{\displaystyle \frac{C}{2}}\right){\sin }^2\varphi$

(F.28)

これらを式(F.18)に代入すると、

$g_m$

$={\displaystyle \frac{GM}{r^2}}-{\displaystyle \frac{3}{2}}{\displaystyle \frac{G}{r^4}}(C-A)\left(3{\sin }^2\varphi -1\right)$

(F.29)

と書ける。 この式は、マカラー (MacCullagh) の式とも呼ばれる。 あるいは、赤道半径を$a$として以下で定義される$J_2$

$C-A\equiv J_{2}M{a}^2$

(F.30)

を用いると、

$g_m$

$={\displaystyle \frac{GM}{r^2}}-{\displaystyle \frac{3}{2}}{\displaystyle \frac{GM{a}^2}{r^4}}{J}_2\left(3{\sin }^2\varphi -1\right)$

(F.31)

とも表される。

地球の自転の角速度の大きさを$\omega$とすると、緯度$\varphi$の点Pにはたらく遠 心力の大きさ$g_{\omega }$は

$$g_{\omega }={\omega }^{2}r\cos \varphi$$

(F.32)

である。 この力は自転軸と垂直な外向きにはたらいていることに注意しよう。 地球の中心に向かう遠心力の成分は

$$-g_{\omega }\cos \varphi =-{\omega }^{2}r{\cos }^2\varphi$$

(F.33)

となる。

重力とは、万有引力による引力と、自転による遠心力との合力であるから、その 加速度$g$は

$$g=\frac{GM}{r^2}-\frac{3}{2}\frac{GM{a}^2}{r^4}{J}_2\left(3{\sin }^2\varphi -1\right)-{\omega }^{2}r{\cos }^2\varphi$$

(F.34)

と書き表わされる。

式(F.31)より、万有引力のポテンシャル$V$を

$$V=-\frac{GM}{r}+\frac{1}{2}\frac{GM{a}^2}{r^3}{J}_2(3{\sin }^2\varphi -1)$$

(F.35)

のように表すことができる。 ただし無限遠($r\to \mathrm{\infty }$)では$V=0$とした。

なおこの式は、引力のポテンシャルの$r^{-3}$以上の高次項を省略した表現になっ ている。 高次項を考慮した場合の引力ポテンシャル $V_1$ は一般に

$$V_1=-\frac{GM}{r}\left[1+\sum _{n=2}^{\mathrm{\infty }}\sum _{m=0}^n{\left(\frac{a}{r}\right)}^n\left(C_{nm}\cos m\lambda +S_{nm}\sin n\lambda \right)P_{nm}(\sin \varphi )\right]$$

(F.36)

と表される。 ここで$P_{n0}$ はルジャンドル関数、$P_{nm}$は (完全正規化された) ルジャ ンドル陪関数である。 また $C_{nm}$ や $S_{nm}$ はストークス係数とも呼ばれ、

$$C_{20}=-J_2,C_{21}=S_{21}=0$$

(F.37)

である。

同様に、遠心力をも含めた重力のポテンシャル $U$ を

$$U=-\frac{GM}{r}+\frac{1}{2}\frac{GM{a}^2}{r^3}{J}_2(3{\sin }^2\varphi -1)-\frac{1}{2}{\omega }^2{r}^2{\cos }^2\varphi$$

(F.38)

のようにとることができる。 遠心力をも含めた重力の等ポテンシャル面のうち、平均海面と一致するものをジ オイドと呼ぶ。

以下では式(F.38)から期待されるジオイド面の表式を求めてみる。 まず赤道($r=a$かつ$\varphi =0$)での重力ポテンシャルの値を$U_0$と書くと

$$U_0=-\frac{GM}{a}\left(1+\frac{1}{2}{J}_2\right)-\frac{1}{2}{\omega }^2{a}^2$$

(F.39)

一方、極($r=c$かつ$\varphi =\pm \frac{\pi }{2}$)でも$U=U_0$となるはずであるか ら、

$$U_0=-\frac{GM}{c}\left[1-{\left(\frac{a}{c}\right)}^2{J}_2\right]$$

(F.40)

である。両者を等値して

$$1+\frac{1}{2}{J}_2+\frac{1}{2}\frac{a^3{\omega }^2}{GM}=\frac{a}{c}\left[1-{\left(\frac{a}{c}\right)}^2{J}_2\right]$$

(F.41)

である。 ここで、以下で定義される偏平率$f$

$$f\equiv \frac{a-c}{a}$$

(F.42)

を求めてみよう。 $f$と$J_2$の2次以上の項を無視すれば、式(F.41)の右辺は

	${\displaystyle \frac{1}{1-f}}\left[1-{\left({\displaystyle \frac{1}{1-f}}\right)}^2{J}_2\right]$	$\approx (1+f)\left[1-(1+2f)J_2\right]\approx (1+f)(1-J_2)$
		$\approx 1+f-J_2$

と書けるので、結局

$$f\approx \frac{3}{2}{J}_2+\frac{1}{2}\frac{a^3{\omega }^2}{GM}$$

(F.43)

を得る。

なお一般的には、基準となるジオイドは回転楕円体とみなして考える。 地球中心からその基準面までの距離を$r_0$と書くと、

$$\frac{r_0{}^2{\cos }^2\varphi }{a^2}+\frac{r_0{}^2{\sin }^2\varphi }{c^2}=1$$

(F.44)

となる。 ここで$a$は赤道半径、$c$は極半径である。 偏平率$f$を用いてこれを書き直すと、

$$\frac{r_0{}^2{\cos }^2\varphi }{a^2}+\frac{r_0{}^2{\sin }^2\varphi }{a^2{(1-f)}^2}=1$$

(F.45)

あるいは

$$r_0=a{\left[1+\frac{2f-f^2}{{(1-f)}^2}{\sin }^2\varphi \right]}^{-1/2}$$

(F.46)

を得る。 式(F.46)を $f$ のベキ級数に展開し、$f$の2次以上の項を無視すれば

	$r_0$	$=a(1-f{\sin }^2\varphi )$		(F.47)
		$=a\left\{1-\left({\displaystyle \frac{3}{2}}{J}_2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{a^3{\omega }^2}{GM}}\right){\sin }^2\varphi \right\}$		(F.48)

と簡略化された表式を得る。 ただし式(F.47で表わされる曲面は回転楕円体ではないことに注意。

基準となるジオイド面上で与えられる基準の重力加速度の値を求めるには、 式(F.48)で与えられた$r_0$を式(F.34)に代入して整理してやれば よい。

この式で、$J_2$ や $a^3{\omega }^2/GM$ に関する高次の項を無視すると

$$g_0=\frac{GM}{a^2}\left(1+\frac{3}{2}{J}_2{\cos }^2\varphi \right)+a{\omega }^2\left({\sin }^2\varphi -{\cos }^2\varphi \right)$$

(F.49)

を得る。