Appendix D 誤差関数

この記述は [10] を参考にした。

誤差関数 (error function) とは以下で定義される。

$$\mathrm{erf}(\eta )=\frac{2}{\sqrt{\pi }}{\int }_0^{\eta }\exp (-\eta {\prime }^2)d\eta \prime$$

(D.1)

同様に補誤差関数 (complementary error function) とは

$$\mathrm{erfc}(\eta )=1-\mathrm{erf}(\eta )$$

(D.2)

で与えられる。 誤差関数はその名や定義式からも想像される通り、正規分布と密接な関係がある。 これに加えて以下に示す通り、誤差関数は熱伝導方程式の解を記述する役割もあ る。 この性質から、誤差関数は熱境界層内の温度分布を簡便に計算する際にもよく登 場する関数である。

以下では、$z>0$ に広がる半無限体を考える。 時刻$t=0$ では内部の温度 $T=T_1$ であったが、時刻$t>0$ では表面$z=0$の温 度が$T=T_0$ に瞬間的に変化を加えたとし、その後の内部の温度変化を考える。 式で書くと、

	${\displaystyle \frac{\partial T}{\partial t}}=\kappa {\displaystyle \frac{{\partial }^{2}T}{\partial z^2}}$		(D.3)
	$\begin{array}{c}T(t=0,z>0)=T_1\hfill \\ T(t>0,z=0)=T_0\hfill \\ T(t>0,z\to \mathrm{\infty })=T_1\hfill \end{array}$		(D.7)

である。 温度$T$をしかるべく無次元化した量として、

$$\theta \equiv \frac{T-T_1}{T_0-T_1}$$

(D.8)

を導入する。 これを用いて方程式を書き直すと、

	${\displaystyle \frac{\partial \theta }{\partial t}}=\kappa {\displaystyle \frac{{\partial }^2\theta }{\partial z^2}}$		(D.9)
	$\begin{array}{c}\theta (t=0,z>0)=0\hfill \\ \theta (t>0,z=0)=1\hfill \\ \theta (t>0,z\to \mathrm{\infty })=0\hfill \end{array}$		(D.13)

である。

熱伝導問題の性質を考慮すると、$\theta$ は$z$と$t$の2つの変数に依存すると いうよりはむしろ、以下で定義される$\eta$の関数として書くほうが簡単になる。

$$\eta \equiv \frac{z}{2\sqrt{\kappa t}}$$

(D.14)

これは、時間 $t$ の間に拡散で熱が伝わる距離 $\sqrt{\kappa t}$ と距離 $z$ との比 (の半分) という意味があることに注意。 これを用いて式(D.9)及び(D.13)を書き直そう。 ここで

	${\displaystyle \frac{\partial \theta }{\partial t}}$	$={\displaystyle \frac{d\theta }{d\eta }}{\displaystyle \frac{\partial \eta }{\partial t}}={\displaystyle \frac{d\theta }{d\eta }}\left(-{\displaystyle \frac{1}{2t}}{\displaystyle \frac{z}{2\sqrt{\kappa t}}}\right)={\displaystyle \frac{d\theta }{d\eta }}\left(-{\displaystyle \frac{\eta }{2t}}\right)$
	${\displaystyle \frac{\partial \theta }{\partial z}}$	$={\displaystyle \frac{d\theta }{d\eta }}{\displaystyle \frac{\partial \eta }{\partial z}}={\displaystyle \frac{d\theta }{d\eta }}{\displaystyle \frac{1}{2\sqrt{\kappa t}}}$
	${\displaystyle \frac{{\partial }^2\theta }{\partial z^2}}$	$={\displaystyle \frac{d}{d\eta }}\left({\displaystyle \frac{\partial \theta }{\partial z}}\right){\displaystyle \frac{\partial \eta }{\partial z}}=\left({\displaystyle \frac{d^2\theta }{d{\eta }^2}}{\displaystyle \frac{1}{2\sqrt{\kappa t}}}\right){\displaystyle \frac{1}{2\sqrt{\kappa t}}}={\displaystyle \frac{d^2\theta }{d{\eta }^2}}{\displaystyle \frac{1}{4\kappa t}}$

であることを用いると、式(D.9)は

$$-2\eta \frac{d\theta }{d\eta }=\frac{d^2\theta }{d{\eta }^2}$$

(D.15)

となり、式(D.13)は

$$\theta (\eta \to \mathrm{\infty })=0,\theta (\eta =0)=1$$

(D.16)

と書き直せる。

式(D.15)を解いてみよう。 その際、まず$\varphi \equiv \frac{d\theta }{d\eta }$ と置いてやると

$$-2\eta \varphi =\frac{d\varphi }{d\eta }\Rightarrow -2\eta d\eta =\frac{d\varphi }{\varphi }$$

(D.17)

これを$\eta$で積分して

$$-{\eta }^2=\ln \varphi -\ln c_1\Rightarrow \varphi =c_1\exp (-{\eta }^2)=\frac{d\theta }{d\eta }$$

(D.18)

を得る。 ここで$c_1$は積分定数である。 これをもう一度$\eta$で積分して

	$\theta$	$=\theta (\eta =0)+c_1{\displaystyle {\int }_0^{\eta }}\exp (-\eta {\prime }^2)d\eta \prime$
		$=c_1{\displaystyle {\int }_0^{\eta }}\exp (-\eta {\prime }^2)d\eta \prime +1$		(D.19)

を得る。 積分定数$c_1$を決めるために、$\eta \to \mathrm{\infty }$の極限をとって、

$\theta (\eta \to \mathrm{\infty })=0$

$=c_1{\displaystyle {\int }_0^{\mathrm{\infty }}}\exp (-\eta {\prime }^2)d\eta \prime +1$

(D.20)

であるが、よく知られたGauss積分の公式より

$${\int }_0^{\mathrm{\infty }}\exp (-\eta {\prime }^2)d\eta \prime =\frac{1}{2}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\exp (-\eta {\prime }^2)d\eta \prime =\frac{\sqrt{\pi }}{2}$$

(D.21)

であるから結局、

$\theta$

$=1-{\displaystyle \frac{2}{\sqrt{\pi }}}{\displaystyle {\int }_0^{\eta }}\exp (-\eta {\prime }^2)d\eta \prime =\mathrm{erfc}(\eta )$

(D.22)

を得る。

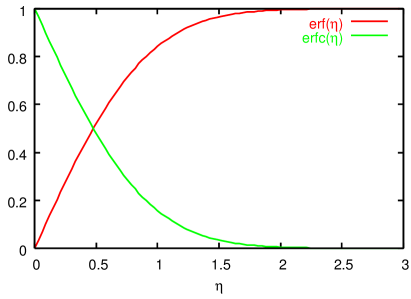
図5に誤差関数$\mathrm{erf}(\eta )$及び補誤差関数 $\mathrm{erfc}(\eta )$のグラフを示しておく。