今回と次回で「数値計算」シリーズ第3弾とて「常微分方程式の数値解法」を。 まずはテキストの第10.1章と第10.2章に沿って、出発点となる話。 さらにテキスト第7.3章に沿って、解法の正確さに関する話をする上で必要となる「テイラー展開」の話を。
常微分方程式の初期値問題その1
地球科学に限らず、自然界の現象の多くは微分方程式で記述されている。
常微分方程式とは
未知関数の導関数を含む関数方程式 を微分方程式という。 その中で、独立変数が1つのもの が常微分方程式である。 独立変数が2つ以上ある微分方程式は「偏微分方程式」という。 科学技術計算で出てくる微分方程式はほとんどが偏微分方程式ではあるが、常微分方程式の数値計算法が理解できれば、偏微分方程式の計算法 (の原理) が理解できたも同然。
常微分方程式の例として、ニュートンの運動方程式 (高校の物理で習うやつ) が挙げられる。 \begin{equation} \fbox{質量}\times\fbox{加速度}=\fbox{力} \quad\text{または}\quad {m}{a}={f} \tag{10.1} \end{equation} も実は微分方程式である。 ある時刻 \(t\) における質点の位置を \(x\)、速度を \(v\) と書くと、 \begin{equation} \fbox{加速度} =\fbox{速度の変化率} =\lim_{\Delta{t}\to0}\dfrac{v(t+\Delta{t})-v(t)}{\Delta{t}} =\dfrac{d{v}}{d{t}} \tag{10.2} \end{equation} であるから、運動方程式は \begin{equation} m\dfrac{d{v}}{d{t}}={f} \tag{10.3} \end{equation} という微分方程式 (「1階の常微分方程式」) に書き直せる。 さらに \begin{equation} \fbox{速度} =\fbox{位置の変化率} =\lim_{\Delta{t}\to0}\dfrac{x(t+\Delta{t})-x(t)}{\Delta{t}} =\dfrac{d{x}}{d{t}} \tag{10.4} \end{equation} であることを使うと、 \begin{equation} \fbox{加速度} =\dfrac{d{v}}{d{t}} =\lim_{\Delta{t}\to0}\dfrac{\dfrac{d{v}}{d{t}}(t+\Delta{t})-\dfrac{d{v}}{d{t}}(t)}{\Delta{t}}=\dfrac{d^2{x}}{d{t}^2} \tag{10.5} \end{equation} なので、結局は \(x\) に関する2階の常微分方程式になる。 \begin{equation} m\dfrac{d^2{x}}{d{t}^2}={f} \tag{10.6} \end{equation}
常微分方程式を解く方法は、積分の計算とほぼ同じ。 例として、\(x\) に関する2階の常微分方程式 \(\dfrac{d^2{x}}{d{t}^2}=-{g}\) を解いてみる。 \(\dfrac{d{x}}{d{t}}=v\) と置くと、もとの方程式は \(\dfrac{d{v}}{d{t}}=-g\) と書き直せる。 両辺を \(t\) で積分すると、 \begin{equation} v=\int\dfrac{d{v}}{d{t}}d{t}=-\int{g}\,d{t}=-{g}{t}+C_1 \quad({C_1}\text{は積分定数}) \tag{10.8} \end{equation} さらに両辺を \(t\) で積分すると、 \begin{align} x=\int\dfrac{d{x}}{d{t}}d{t}=\int{v}\,d{t}& =\int\left[-{g}{t}+C_1\right]d{t} =-\dfrac{1}{2}{g}t^2+C_1{t}+C_2 \quad({C_2}\text{は積分定数}) \tag{10.9} \end{align} となる。 これより、以下のことが確認できる。
- 高階の常微分方程式でも、階数の高い微分係数から順序よく 扱えばOK。 1階の連立常微分方程式に書き直して解くことができる。
- 積分定数を決めるためには、別の条件を課す必要がある。 例えば「\(t=0\) で \(x=x_0\) かつ \(v=v_0\)」など。 これを 初期値 といい、与えられた初期値のもとで解を求める問題を 初期値問題 という。 初期条件は、積分定数の数、言い換えれば常微分方程式の階数だけ必要。
以下、常微分方程式の初期値問題を数値的に解く方法をいくつか紹介する。 後に出てくるものほど、手間はかかるが、正確さに優れている。
オイラー法
常微分方程式 \(\dfrac{d{x}}{d{t}}=f(t,x)\) を \({a}\le{t}\le{b}\) の範囲で、初期条件 \(x(t=a)=x_0\) のもとで解くことを考える。 第11回の「数値積分」の時と同様に、解を求めたい範囲 (例えば \({a}\le{t}\le{b}\)) の間にいくつかの点 \(t=t_0,t_1,\cdots,t_N\) をとり、各 \(t_i\) における \(x\) の近似値を求めることにする。 点の間隔を \(h=\dfrac{b-a}{N}\)とかくと、 \begin{equation} t_i=a+{h}{i}=a+\dfrac{b-a}{N}i\quad(i=0,1,\cdots,N) \tag{10.10} \end{equation}
オイラー法の手順は以下。
- \(t=t_0\) での \(x\) の値 \(x_0\) は、初期条件として与えられているとする。
- \({t}\le{t_i}\) の点での \(x\) の値 \(x_i\) が既に求まっているとする。
- 次の式により、\(t=t_{i+1}\) での \(x\) の値 \(x_{i+1}\) を計算する。 \begin{equation} x_{i+1}=x_{i}+{f(t_i,x_i)}\times{h} \tag{10.11} \end{equation}
- 全ての範囲で解が求まったらOK。
オイラー法の意味
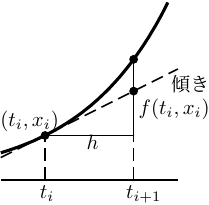
ある点で曲線の接線を引くと、その接点のごく近くだけを見れば、接線と元の曲線とはとてもよく似ているという話がここでも登場する。 右図 (図10.1も参照) より \begin{align} \fbox{点 \((t_i,x_i)\) における接線の傾き \(\dfrac{dx}{dt}\)} &=f(t_i,x_i)\notag\\& \simeq\dfrac{x_{i+1}-x_{i}}{t_{i+1}-t_{i}}=\dfrac{x_{i+1}-x_{i}}{h} \tag{10.12} \end{align} 即ち点 \((t_i,x_i)\) を通る接線に沿って \(t\) を \(h\) だけ進めた点を \(x_{i+1}\) にとっている。
オイラー法についての補足
当然ながら、「小区間の幅」が小さいほうが計算の正確さは増すものの、実際の問題に適用するには正確さの増す「スピード」が重要になる。
- オイラー法では、真の答からのずれが「小区間」の数の1乗に反比例して減少 する。
- この「スピード」では実用的な問題には向かない
- 正確さを10倍増すには、「小区間」の数を10倍にする必要がある。 その分だけ手間と時間がかかる。
- しかし 第09回の「情報落ち」の影響により、「小区間」の幅を小さくしても正確さが増すとは限らない。
テイラー展開、テイラー級数
微分方程式の数値解法の精度という話をするには、どうしてもテイラー展開を避けては通れない。 また理系の大学生である以上は「常識」として知っていてほしいものでもある。
- ある関数 \(F(x)\) が \(x=x_i\) の近傍で連続かつ無限回微分可能であるとすると、 \begin{align} F(x=x_i+h)&=\sum_{n=0}^{\infty}\dfrac{F^{(n)}(x=x_i)}{n!}{h^n} \tag{7.28} \\& =F(x=x_i)+{F\prime(x=x_i)}{h}+\dfrac{1}{2}{F\prime\prime(x=x_i)}{h^2}+\cdots \tag{7.29} \end{align} と書ける。 これを 「\(x=x_i\) のまわりでのテイラー展開」などという。
- ちなみに、\(x=0\) のまわりでテイラー展開したもの
\begin{equation}
F(x)=\sum_{n=0}^{\infty}\dfrac{F^{(n)}(x=0)}{n!}{x^n}
\tag{7.31}
\end{equation}
を特に「マクローリン展開」という。
マクローリン展開の例として有名なものは、
- 指数関数: \(F(x)=e^x\) とすると、\(F^{(n)}(x=0)=e^x(x=0)=1\) だから \begin{align} e^x=\sum_{n=0}^{\infty}\dfrac{x^n}{n!}& =\dfrac{x^0}{0!}+\dfrac{x^1}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\dfrac{x^5}{5!}+\dfrac{x^6}{6!}\cdots \tag{7.32}\\& =1+{x}+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}+\dfrac{x^5}{120}+\dfrac{x^6}{720}\cdots \notag \end{align}
- テイラー展開の最初のいくつかの項だけを考えてやることにより、\(x=x_i\) のまわりでの関数 \(F(x)\) の変化を近似する ことができる。
その例が図7.2。
- 最初の2つの項 (\(h^1\) まで) を考えると、直線で近似 したことになる。
- 最初の3つの項 (\(h^2\) まで) を考えると、2次関数で近似 したことになる。
- オイラー法は「最初の2つの項」までを考えた直線近似に基づいて計算したことになっている。
それゆえオイラー法では
- 正確さの増すスピードが遅い (小区間の数の1乗にしか反比例してくれない)
- 直線的な変化であれば完全に合わせることができるけれど、直線的でない変化はうまく合わせられない (図10.2)。
テイラー展開で最初の3つ以上の項まで正しく取り込んだ方法を使えば、オイラー法よりも正確に計算ができるはずである。 次回はそのような方法の例として、ホイン法 (修正オイラー法)・中点法 (改良オイラー法)とルンゲ-クッタ法を紹介する。