後半戦の数値計算シリーズの第2弾として、テキスト第9章に沿って数値積分の話を。
数値積分
\(S=\displaystyle\int_{a}^{b}f(x)dx\) のような積分 (「定積分」) の計算をしたいという欲求は、科学技術計算の多くの場面で現れる。
定積分の計算とは
これまでは、\(\dfrac{d}{dx}F(x)=f(x)\) (式(9.1)) を満たすような関数 \(F(x)\) (「不定積分」あるいは「原始関数」) をどうにかして求めてから、定積分の計算を行ってきたはずだ。 しかし実際の問題では、不定積分 \(F(x)\) が簡単に求まらない 場合が多い。 そこで、コンピュータを使った近似的な定積分の計算が必要になる。
そもそも「定積分」とは何か? それを考えるには、どんな場面で登場してきたか? を思い出してみるとよい。
- グラフで囲まれた 領域の面積を求める ことと同じ。
- 「いびつ」なグラフであっても、多数の細い「短冊」状の領域に分けて、それらの面積をたし合わせる と求まる (区分求積法; 図9.2)。
- 使用する「短冊」が細く、数が多いほど、より正確な値が求まるはず。
ここまでの話を数式で書き下しておく、 積分区間 \({a}\le{x}\le{b}\) を \(N\) 等分してできる「短冊」を考える。 「短冊」の幅を \(h=\dfrac{b-a}{N}\)、\(i\) 番目の「短冊」が表す区間を \(x_{i-1}\le{x}\le{x_i}\) と書く。(ただし \(x_0=a\) かつ \(x_N=b\)とする。) 関数 \(y=f(x)\) のグラフを区切って作った \(i\) 番目の「短冊」の面積を \(S_i\) と書くと、\(N\) 個の「短冊」の面積の総和 \(S_N\) は \begin{equation} S_N\equiv\sum_{i=1}^{N}S_i \tag{9.4} \end{equation} であり、\(N\to\infty\) としたときの \(S_N\) の極限として定積分 \begin{equation} S\equiv\int_{a}^{b}f(x)dx=\lim_{N\to\infty}{S_N} \tag{9.5} \end{equation} の値が求まる。 とはいえ実際の数値計算では \(N\) を無限大にとることはできないので、有限な個数 (\(N\) 個) の「短冊」の面積の総和 \(S_N\) を使って、求めたい定積分 \(\displaystyle\int_{a}^{b}f(x)dx\) の値を近似的に求めることになる。 その際、個々の「短冊」状の部分の面積をどう求めるか? によっていくつもの方法に分かれる。
台形則 (trapezoidal rule)
この方法が最も単純かつ基本的。
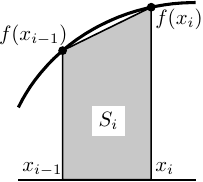「台形則」では、\(i\) 番目の「短冊」の面積 \(S_i\) を 台形の面積の公式
から求める。
右図 (図9.3も参照) より
\begin{equation}
S_i=\frac{f(x_{i-1})+f(x_i)}{2}h
\tag{9.6}
\end{equation}
ここでも、「短冊」の幅が十分小さければ、その間での関数 \(f(x)\) の変化は直線状だとみなしてよい ことを用いている。
式(9.6)を式(9.4)に代入して、さらに変形すると、 \begin{align} \int_{a}^{b}f(x)dx& =\sum_{i=1}^{N}\frac{f(x_{i-1})+f(x_i)}{2}h ={h}\frac{1}{2}\sum_{i=1}^{N}[f(x_{i-1})+f(x_i)] \notag\\& ={h}\left[\frac{1}{2}f(x_0)+\sum_{i=1}^{N-1}f(x_i)+\frac{1}{2}f(x_N)\right] ={h}\left[\frac{1}{2}f(a)+\sum_{i=1}^{N-1}f(x_i)+\frac{1}{2}f(b)\right] \tag{9.7} \end{align} となる。 よくある教科書では、この表式が載っている。
中点則
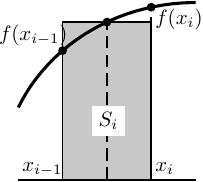中点則では、個々の「短冊」の面積 \(S_i\) を以下の表式により求める。
\begin{equation}
S_i=(x_{i}-x_{i-1})\times{f(x=\frac{x_{i-1}+x_{i}}{2})}
\tag{9.8}
\end{equation}
右図 (図9.4も参照) より、個々の「短冊」を幅が \(h\) (\(=x_{i}-x_{i-1}\))、高さが \(f(x=\displaystyle\frac{x_{i-1}+x_{i}}{2})\) の長方形だとみなして面積を求めていくのが中点則である。
シンプソン法
シンプソン法とは、となりあう「短冊」2つ分にわたる関数の変化を2次関数であてはめることにより、定積分を求める方法である。
「短冊」の個数 \(N\) が偶数であるとし、\(m=N/2\) とおく。 区間 \({x}_{2j-2}\le{x}\le{x}_{2j}\) における関数 \(f(x)\) の変化をあてはめた2次関数を \(\tilde{f}(x)\) と書くと \begin{equation} S_{2j-1}+S_{2j}=\int_{x_{2j-2}}^{x_{2j}}\tilde{f}(x)dx \tag{9.10'} \end{equation} により計算する。 ここで、あてはめる2次関数 \(\tilde{f}(x)\) は \begin{equation} \tilde{f}(x) =\frac{{f(x_{2j})}-2{f(x_{2j-1})}+{f(x_{2j-2})}}{2h^2}(x-x_{2j-1})^2 +\frac{{f(x_{2j})}-{f(x_{2j-2})}}{2h}(x-x_{2j-1}) +{f(x_{2j-1})} \tag{9.9} \end{equation} で計算できる。 この式は「ラグランジュ補間」の式(7.20) と、「求める2次関数が3つの点 \((x_{2j-2},f(x=x_{2j-2}))\)、\((x_{2j-1},f(x=x_{2j-1}))\)、\((x_{2j},f(x=x_{2j}))\) を通る」という条件から即座に導かれる。 ここで \(t\equiv{x-x_{2j-1}}\) と変数変換し、\(x_{2j}-x_{2j-1}=h\) かつ \(x_{2j-2}-x_{2j-1}=-h\) であることを用いて、式(9.10')の式変形の続きを進めると、 \begin{align} S_{2j-1}+S_{2j}& =\frac{{f(x_{2j})}-2{f(x_{2j-1})}+{f(x_{2j-2})}}{2h^2}\int_{-h}^{h}t^2dt +\frac{{f(x_{2j})}-{f(x_{2j-2})}}{2h}\int_{-h}^{h}tdt +{f(x_{2j-1})}\int_{-h}^{h}dx \notag\\& ={h}\frac{{f(x_{2j})}+4{f(x_{2j-1})}+{f(x_{2j-2})}}{3} \tag{9.11} \end{align} となる。 なおこの式変形の最後において、「偶関数」と「奇関数」の性質がうまく利用されていることに注意。
さらに、全ての「短冊」の面積の総和をとると \begin{equation} \sum_{i=1}^{N}S_i=\sum_{j=1}^{m}\left(S_{2j-1}+S_{2j}\right) =\frac{h}{3}\left[f(x_0)+f(x_{N}) +2\sum_{j=1}^{m-1}f(x_{2j}) +4\sum_{j=1}^{m}f(x_{2j-1})\right] \tag{9.12} \end{equation} を得る。 よくある教科書では、この表式が載っている。
数値積分法についての補足
- 原理的には、「短冊」の幅が小さいほうが正確さが増す。
- 台形則や中点則では、真の答からのずれが「短冊」の数の2乗に反比例して減少する
- シンプソン法では、真の答からのずれが「短冊」の数の4乗に反比例して減少する。
- 台形則もシンプソン法も、「ニュートン・コーツ型」と呼ばれる数値積分法の一種。 どちらも、多項式の定積分により「短冊」の面積を求めるところからスタート (台形則は1次関数、シンプソン法は2次関数)。 一般的には、偶数次の関数を使った数値積分法のほうが精度がよいとされる (真の答からのずれの減少のしかたが速い)。
- ただし、あまりにも次数の高い多項式で「あてはめ」て定積分の計算をしてはいけない。
- 次数の高い多項式では、それだけ多数の極大・極小が表われる。
あてはめた関数が不必要な凸凹を人工的に作り出してしまう恐れが大。
- 次数の高い多項式では、それだけ多数の極大・極小が表われる。
- 多くの場合は、「短冊」を十分に細かくとって「台形則」を使えばOK。