今回から後半戦の「数値計算」シリーズに入りたい。
- 地球物理学的現象の数値シミュレーションも含めて、物理現象のシミュレーションとはだいたい「知りたい現象を記述する方程式を解く」作業を伴う。
- 現れる方程式はだいたい、手計算で解くことが難しい or 不可能
- 3つ以上の物体が関わる運動方程式 (太陽系の惑星の運動)
- 流体力学のナビエ・ストークス方程式 (海洋物理、マントル対流)
- 量子力学のシュレディンガー方程式 (第一原理分子動力学)
- 仕方がないので、コンピュータに代わりに解いてもらおう。
この講義の後半戦では、ある与えられた方程式を、コンピュータに解かせるための方法 (のうち、ごく基本的なもの) として、
- 非線形方程式を解く (テキスト第8章)
- 定積分を計算する (テキスト第9章)
- 常微分方程式を解く (テキスト第10章)
今回はテキスト第8章に沿って、非線形方程式を数値的に解く方法について、代表的なものを紹介する。
非線形方程式の数値解法
非線形方程式とは、「線形でない」方程式のこと。
- 線形方程式とは \(ax+b=0\) のようなもの。 解くべき変数 (\(x\)) の1次の項までしか出てこない式。 グラフを描いたら直線になる。
以下、非線形方程式 \(f(x)=0\) の解 (\(f(x)=0\) を「近似的に」満たす \(x\) の値) を求める方法を2つ紹介する。 いずれも「一発で」解を求めるものではなく、目星をうまくつけながら「逐次的に」(だんだんと) 求める解に近づいていくための方法である。
二分法
非線形方程式 \(f(x)=0\) の解が \({a_0}<{x}<{b_0}\) の範囲に1つだけあると「あらかじめ」分かっているとする。 具体例でいうと、 \begin{equation} \begin{split} \text{$f(x)$ が ${a_0}\le{x}\le{b_0}$ で単調 (単調増加あるいは単調減少) で、}\\ \text{かつ $f(x=a_0)$ と $f(x=b_0)$ が異符号}\\ \end{split} \tag{8.1} \end{equation} である場合を考える。 なおこの条件は決して厳しいものではないことを注意しておく。 なぜなら、\(y=f(x)\) のグラフをあらかじめ描いておくなどの手段によって、「解の1つはこの範囲にありそうだ」という予想をたてることは十分可能であるから。
二分法の手順
- \(i\) 回目のくり返し計算において、\({a_i}<{x}<{b_i}\) の範囲で関数 \(f(x)\) が単調であり、かつ \(f(x=a_i)\) と \(f(x=b_i)\) の符号が異なるような2つの数 \(a_i\) と \(b_i\) を用意する。
- \(x_i=\dfrac{a_i+b_i}{2}\) に対して \(f(x_i)\) を計算する。
- \(f(x=x_i)\) の符号によって条件分岐。 (図8.1参照)
- \(f(x=x_i)\) と \(f(x=a_i)\) の符号が同じならば、\({a_i}<{x}\le{x_i}\) の範囲に解はない。
次は \({x_i}<{x}\le{b_i}\) の範囲を探せばよいから、 \begin{equation} a_{i+1}\Leftarrow{x_i} ,\quad b_{i+1}\Leftarrow{b_i} \tag{8.2} \end{equation} としてやる。 - \(f(x=x_i)\) と \(f(x=b_i)\) の符号が同じならば、\({x_i}<{x}\le{b_i}\) の範囲に解はない。
次は \({a_i}<{x}\le{x_i}\) の範囲を探せばよいから、 \begin{equation} a_{i+1}\Leftarrow{a_i} ,\quad b_{i+1}\Leftarrow{x_i} \tag{8.3} \end{equation} としてやる。
- \(f(x=x_i)\) と \(f(x=a_i)\) の符号が同じならば、\({a_i}<{x}\le{x_i}\) の範囲に解はない。
- 十分正確な解が求まったらOK、求まっていなければもう一度くり返す。
二分法の性質
式(8.1)の2つの条件を満たしてさえいれば、\(f(x)=0\) を解くのに二分法が使える。 しかも、最初に与える範囲 \(b_0-a_0\) がどれだけ広かったとしても、(計算の手間を十分にかけさえすれば) 求めたい解が必ず得られる。 この意味で、二分法は安全確実な方法だが、正解へたどり着く (収束する) 速さは一般に遅い。
ニュートン法
関数 \(f(x)\) の表式が分かっていて、しかも \(f(x)\) の微分が簡単に計算できる ならば、ニュートン法 (Newton-Raphson 法とも) を使うのがよい。
ニュートン法の手順
ある値 \(x_0\) からくり返し計算を開始するとする。
- \(i\) 回目のくり返し計算において、「近似的な」解 \(x_i\) をとる。
- 次の式により、\(i+1\) 回目の「近似的な」解 \(x_{i+1}\) を計算する。 \begin{equation} x_{i+1}=x_{i}-\dfrac{f(x_{i})}{f'(x_{i})} \tag{8.5} \end{equation}
- 十分正確な解が求まったらOK、求まっていなければもう一度くり返す。
ニュートン法の意味
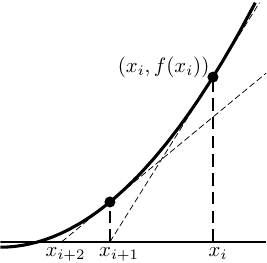右図 (図8.3も参照) をもとに、ニュートン法の手順に含まれる式(8.5)の意味を考えてみる。
\(y=f(x)\) のグラフにおいて、曲線上のある点 \((x_i,f(x=x_i))\) を通る接線の方程式は
\begin{equation}
y=f'(x=x_i)\times(x-x_i)+f(x=x_i)
\tag{8.6}
\end{equation}
これに \(x=x_{i+1}=x_{i}-\dfrac{f(x_{i})}{f'(x_{i})}\) を代入すると、
\begin{equation}
y=f'(x=x_i)\times\left[-\dfrac{f(x_{i})}{f'(x_{i})}\right]+f(x=x_i)=0
\tag{8.7}
\end{equation}
即ち \(x_{i+1}\) は、曲線 \(y=f(x)\) 上の点 \((x_i,f(x_i))\) における 接線が \(x\)-軸と交わる点の位置 である。
ニュートン法の背景にある考え方とは
- どんな曲線のグラフでも、ごく限られた狭い範囲だけを見れば、ほぼ直線である。
- すなわち、ある点で曲線の接線を引くと、その点の近くだけを見れば、接線ともとの曲線とはとてもよく似ている。
- それゆえ、もとの曲線のグラフと \(x\) 軸との交点を探す代わりに、もとの曲線の接線と \(x\) 軸との交点を探す ことで、近似的な解を考えることにする。
非線形の世界でも、ごく小さな領域だけをみれば、ほぼ線形の世界であるということができる。 このような考え方は、数値計算の世界で非常によく用いられるものである。
ニュートン法の性質
- ニュートン法は (もし収束するならば) 二分法よりも速い。
- ニュートン法がうまく使えるためには、真の解に近いところからくり返し計算を開始する のが重要。 真の解からあまりにも離れたところから始めると、収束しないことがある。
- 特に、\(f'(x)\) が \(0\) に近くなるような \(x_i\) が現れるときは発散の恐れが高い。
例えば
- \(y=\log(x)-1\) を大きな正の \(x\) から解き始める場合。
- 重解が出てくる場合 (この場合は二分法でも大変)。
どの解法を使うべきか? (についての亀山の私見)
以下、代表的な「二分法」と「ニュートン法」で比べてみると、
簡単ながらも安全確実な二分法をまず試してみるべしというのが現在の亀山の私見。 なおその昔 (亀山が学生だった頃) は
一般的には収束の速いニュートン法を使うべき。ただし、ニュートン法が使えない (\(f'(x)\) が分からないなど) 場合には、二分法でもOKと教えられてきた。 だが計算機の性能が格段に向上した最近では、ニュートン法の優位性も低下してきたような気が (亀山には) している由。
とはいえ、どの方法を使うにせよ、解きたい \(f(x)\) の性質をあらかじめ知っておくことが 大事。
- 設定を間違ったら、いくらやっても収束しないこともある
安全確実な二分法であっても、「解の存在する範囲」の最初の指定を間違うと、正しい答に到達しない。 - 当然「真の解」に近いところからスタートするほうが速い