マントル対流理論の基礎 (第10.5章)
熱対流とは (第10.5.1章)
温度差によって引き起こされる対流を「熱対流」という。 お風呂の中のお湯などでも熱対流が起こっている。
地球のマントルの中の運動も、熱対流とよく似ている。
- 高温の上昇流 ↔ 上昇プルーム
- 表面の水平流 ↔ プレート運動
- 低温の下降流 ↔ 沈み込み
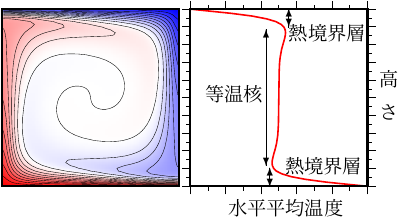まず、対流の構造 (右図; 図10.22) に関する重要な用語を紹介する。
- 対流胞 (対流セル)
- 上昇流と下降流で区切られた「小部屋」のような構造。
- 等温核
- 対流胞の中心付近にできる、温度がほとんど一定の部分。
- 熱境界層
- 対流胞の上下の境界に沿って薄い層状にできる、温度の変化が大きい部分。
なおこの図の場合では、等温核の温度は深さによらずほぼ一定になっているが、(固体地球物理学に限らず) 地球科学で登場する対流ではこれとは (いくぶん) 異なった温度変化になっていることが多い。 例えば大気の層の中を空気塊が (断熱的に) 上昇する場合を考えてみると、上層にいくほど圧力が低くなり、体積が増加する (第10回で登場した圧縮と同じ) ことによって温度は下がってしまう。 この温度変化の度合は「断熱温度減率」と呼ばれているのであった。 ちなみに「フェーン (Foehn) 現象」は、空気塊の断熱温度減率が水分を含んだ場合 (「湿潤温度減率」; 約 6.5 K/km) と含まない場合 (「乾燥温度減率」; 約 10 K/km) で異なることが原因で起こっている。
これと同じようなことは固体地球の中でも起こっており、熱境界層から遠く離れたところでも深さとともに圧力が高くなれば温度も増加する。 固体地球科学分野ではこの温度変化の度合は一般に「断熱温度勾配」と呼ばれている。 ただし固体地球を構成する物質は大気と比べれば非常に圧縮されにくいことから、断熱温度勾配の値は大気のそれよりも圧倒的に小さい。 実際、地球のマントルの断熱温度勾配は地温勾配と比べるとかなりゆるやかなもので、約 0.3 K/km と見積られている (くわしい話は後期の「固体地球物理学」で)。
地球内部で熱対流は起こるか?
温度差による浮力で上昇流が発生する場合を考える (第10.5.2b章)。
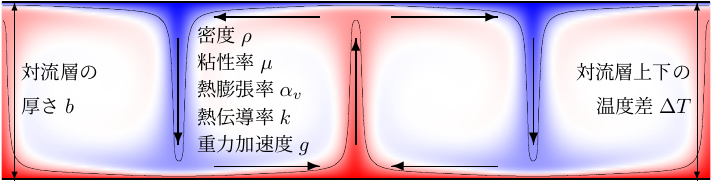
- Rayleigh による理論的な研究 (1916年) の結果によると、熱対流が起こるかどうかは、「レイリー数 (Rayleigh number)」という指標によって判定できる。 \[ {Ra}=\dfrac{\fbox{対流させようとする効果の強さ}}{\fbox{対流を抑えようとする効果の強さ}} \]
- 上図 (図10.24) に示した設定のもとでは
- 対流させようとする効果をもつもの:
- 上下の温度差 (\(\Delta{T}\))、流体の熱膨張 (\(\rho\alpha_v\))、重力加速度 (\(g\)) ← 浮力を大きくする
- 流体層の厚さ (\(b\)) ← 伝導による熱輸送の効率を下げる
- 対流を抑えようとする効果をもつもの
- 流体の粘性 (\(\mu\)) ← 流体を動きにくくする
- 流体の熱伝導率 (\(\kappa\equiv{k/\rho{c_p}}\)) ← 伝導による熱輸送の効率を上げる
- 対流させようとする効果をもつもの:
- この設定のもとでは、熱対流のレイリー数 \(Ra\) は
\begin{equation}
{Ra}\equiv\dfrac{\rho\alpha_v\Delta{T}{g}b^3}{\mu\kappa}
\tag{10.37}
\end{equation}
と定義される。
ただし
- \(\alpha_v\) は熱膨張率 (温度による密度の変化率)、
- \(\kappa\equiv\dfrac{k}{\rho{c_p}}\) は熱拡散率 (熱伝導による温度の変化のしかたに関係)、
- \({c_p}\) は比熱 (単位質量の物質の温度を1K上げるのに必要な熱エネルギー)。
定義より、レイリー数 \(Ra\) が大きいほど、対流が起こりやすくなるはず。
- 対流が起こる場合と起こらない場合とを分けるレイリー数の値を「臨界レイリー数」 (\(Ra_c\)) という。 臨界レイリー数 \(Ra_c\) の値は条件によって異なる (図10.25) のだが、おおよその大きさは \(10^3\) 程度である。
- 表10.3に示した値を用いて計算すると
- 地球マントルの \(Ra\) はだいたい \(10^7\) 程度と見積られており、臨界レイリー数 \(Ra_c\) よりも十分大きい。
かくも大きな粘性でも熱対流が起こるのは、マントルが非常にぶ厚いから。 (\(Ra\propto\fbox{流体層の厚さ}^3\)) - 地球外核の \(Ra\) は \(10^{30}\) 程度で、かなり激しい対流が起こると予想される。 ただし実際には、外核の対流は「地球が自転している」効果を強く受けて起こっている。その場合には臨界レイリー数が \(10^3\) よりも大きくなるため、外核の対流はそこまで激しいものではないかも知れない。
- 地球マントルの \(Ra\) はだいたい \(10^7\) 程度と見積られており、臨界レイリー数 \(Ra_c\) よりも十分大きい。
対流の激しさとレイリー数 (第10.5.3章)
レイリー数 \(Ra\) が大きくなるほど対流は激しくなると予想される。
- \(Ra\) が大きくなると、熱対流の構造に変化が生じる (図10.26)。
- 高温の上昇域・低温の下降域が細くなる
- 熱境界層が薄くなる
- 熱境界層の中の温度勾配が大きくなる
- \(Ra\) が大きくなると、対流によって運ばれる熱量が増える。
- 対流による熱輸送の効率は、ヌッセルト数 (\(Nu\))という指標ではかられる。 \begin{equation} Nu=\dfrac{\fbox{対流による熱流量}}{\fbox{伝導による熱流量}} \tag{10.38} \end{equation}
- \(Ra\) が10倍大きくなると、\(Nu\) はおよそ 2.1 (\(=\sqrt[3]{10}\)) 倍になる (図10.27a)。
- \(Ra\) が大きくなると、対流による流れが速くなる。
- \(Ra\) が10倍大きくなると、流速はおよそ 4.6 (\(=\sqrt[3]{100}\))倍になる (図10.27b)。
レイリー数 \(Ra\) が \(10^7\) 程度の熱対流を考えれば、地球の表面で得られている観測量
- 対流が運ぶ熱量 (約 87 mW/m2)
- 表面での流速 (数 cm/年)
「熱対流」のその先へ: 地球惑星の内部のよりリアルな描像に向けて
ここまでの議論では、簡単な設定のもとで起こる熱対流の性質を紹介してきた。 具体的には、2次元の箱型の容器の中で起こる、
- 粘性率や熱膨張率などの物性が一定で、
- 相状態や化学組成が一定で、
- 時間変化のない定常状態での対流、
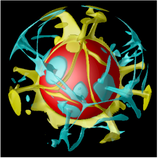これに対し、実際の地球内部で起こっている対流現象には、3次元の「まるい」球殻の中で起こることに加え、
- 温度や圧力などの変化によって、粘性率や熱膨張率などの物性が変化する、
- 温度や圧力などの変化によって、相状態や化学組成が変化する、
- 時間変化のある非定常状態、