固体地球物理学概論 (2024年前学期) 第9回

固体地球内部の熱的状態 (第10.4章+第8.2章+第8.3章)

熱を伝えるには、3つの手段がある。

• 伝導: ふれあったモノの間で伝わる (モノの移動を伴わない)
• 対流: モノが移動することによって伝わる
• 放射: 光 (電磁波) のエネルギーとして伝わる

ただし、放射は地球内部の熱輸送にほとんど効かないので、伝導と対流のみ考えれば十分。

地球表面付近での熱の伝わり具合 (第8.3章)

• 一般的に、地下の温度は地表からの深さとともに増加する。 この傾きを「地温勾配 (geothermal gradient)」という。
• 地温勾配の値は場所によってばらつきはあるものの、典型的にはだいたい 30 K/km 程度の値を示す (図8.3)。(だいたい「100 m につき 3°C」)
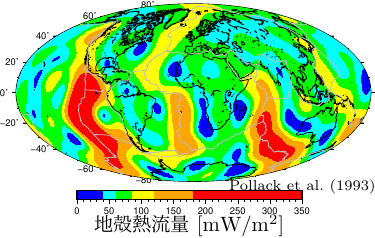
• 地表面で測った熱流量を「地殻熱流量」と呼ぶ。
  平均で約 87 mW/m² (\(0.087\) W/m²; 1平方メートルあたり 0.087 ワット = 87 ミリワット) (全球が図8.4あるいは右図、日本周辺が図8.6)。
• 地球表面全体から放出されている熱の総量はおよそ \(4.4\times10^{13}\) W (44テラワット)

  太陽定数 (地球の大気圏に垂直に入ってくる単位面積あたりの太陽放射のエネルギー) はおよそ 1366 W/m² と見積られている。 これと比べれば地下からくる熱はとても小さいけれど、地球の表面積全体を考えたら、けっこう大量の熱が来ている。

こんな大量の熱はどうやって地球の中からやって来たのか? を考えよう。

伝導による熱輸送 (第10.4.1章)

温度の異なる物体がふれ合っているとき、両者が ふれ合っている面を通して、高温側から低温側へと熱が流れる 現象を熱の「伝導 (conduction)」という。

• 熱伝導における Fourier の法則

  単位時間あたりに単位面積を流れる熱エネルギー \(q\) (熱流量)は、その場所におけるその方向の温度勾配に比例する。

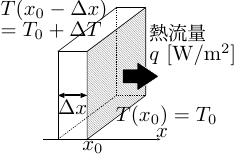  Fourier の法則より、図10.18 (右図) の斜線の面を流れる熱流量 \(q\) は \begin{equation} q=-k\dfrac{T_{(x_0)}-T_{(x_0-\Delta{x})}}{\Delta{x}}=k\dfrac{\Delta{T}}{\Delta{x}} \tag{10.8} \end{equation} あるいは微分を使うと \begin{equation} \vec{q}=-k\nabla{T} =\left(-k\frac{\partial{T}}{\partial{x}},-k\frac{\partial{T}}{\partial{y}},-k\frac{\partial{T}}{\partial{z}}\right) \tag{10.9} \end{equation} のように表わされる。 ちなみに \(\nabla\) は「ナブラ」と呼ばれる微分演算子である。ひとまず今のところは、「それぞれの方向への変化率を成分とするようなベクトルを作るもの」という感じで理解してくれれば OK である。
• Fourier の法則で、右辺に現われる比例定数 \(k\) は「熱伝導率 (thermal conductivity)」と呼ばれ、[W/m K] という単位をもつ。 熱伝導率 \(k\) の典型的な値 (表8.5参照) は、
  • 地表付近の岩石では約 \(2\sim3\) W/m K
  • マントル岩石では約 \(4\) W/m K

もし地球深部のどこまでも伝導で熱が伝わっているとするならば、

• 深さとともに一定の地温勾配 (約 30 K/km) で温度が上がり続けるはずで、
• マントル内 (深さ 2900 km) で岩石の融点をはるかに超えるような高い温度に到達する

ことになってしまうのだが、もちろん実際にはそんなことになっていない (マントルの大部分が固体であることに矛盾)。 すなわち、地球深部では伝導が主要なメカニズムではない。

進んだ話題: 「伝導による半無限体の冷却」モデルと固体地球科学への応用 (第8.4.1章)

熱伝導による物体の冷却を記述する物理モデルの1つとして、「半無限体」というものがよく用いられる。 半無限体とは、「地表面より下は前後左右と無限に広がっているけれど、地表面より上には何もない」というような (理想化された) ものを指す。 固体地球科学で半無限体が登場する代表的な場面が「伝導による半無限体の冷却」であり、高温の岩石がある時刻に冷たい物体と接触した (マグマが岩盤の中に貫入した、上昇してきたアセノスフェアが地表面の中央海嶺まで到達した、など) 場合に、その後の岩石の内部の温度が低下していく経過をたどるような問題を簡略化したものにあたる。

この「伝導による半無限体の冷却」の問題は解析的に (手計算で) 解けることが知られており、その解は図8.10 などのように与えられる [mp4 動画]。 時間の経過とともに、冷やされた部分の幅がどんどん大きくなり、しかもその部分の温度の変化率がゆるやかになっていく様子が見てとれるだろう。 さらに詳しく調べてみると、地表面での温度勾配の値は、冷却を受けた時間の平方根に反比例して小さくなっていることも分かる。 この結果は 第3回でみた、(年代がそんなに古くない) 海洋プレートの特徴がその年代によって変化する傾向 (業界用語で「\(\sqrt{t}\) 則」などという) をうまく説明できるものであり、伝導による冷却が海洋プレートの成長を規定している要素の1つであることを意味している。

この問題は19世紀の半ばに Lord Kelvin (ケルビン卿; 1824〜1907; イギリス) が地温勾配に基づいて地球の年齢を見積ろうとする試みの中でも用いられた。 その際 Kelvin は、地球は初期の非常に高温の状態から、伝導による冷却を受けて現在に至ったと考えた。 当時知られていた値 (地温勾配 25 K/km など) と半無限体の冷却による地温勾配の時間変化とを比較することにより、Kelvin は地球の年代を約6500万年と見積った。 もちろんこの見積りは正しくないのだが、その理由は以下に挙げるような効果を考えていないことにある。 ただしこの見積りは実は海洋プレートの年代を見積る手順に相当するものであり、得られた値は確かに海洋プレートの平均的な年代とほぼ等しい。

地球内部の熱源 (第8.2.2章+第10.4.2章)

プレートテクトニクスに代表される地球の活動は、地球が持っている熱エネルギーを原動力として起こっている。 さらに、その地球の熱エネルギーの起源にも大きく分けて2種類が考えられる。 その1つは、地球ができた時にもともと持っていた「始原的 (primordial)」な熱で、微惑星などの衝突・集積によって地球ができる際に重力のエネルギーが熱に変換されて生じたもの。(破片がバラバラに分布している状態から、密集して分布する状態に変わる際に、重力のエネルギーは小さくなる。その減った分の一部が熱に変換されたもののことを指している。) もう1つは、地球の内部で時々刻々と発生しているもので、以下ではこの熱について考える。

• 地球の内部は放射性元素の崩壊による加熱を受けている。 その仕組みは原子炉と同じ。
• 代表的な放射性元素と、その同位体は
  • U (ウラン): このうち ²³⁸U (天然ウランの99.28%) と ²³⁵U (0.71%)
  • Th (トリウム): ²³²Th
  • K (カリウム): このうち ⁴⁰K (天然カリウムの0.0119%)
  上の3つの放射性元素はいずれも、10億年程度の半減期をもっており、地球内部で長時間にわたって発熱する。(表8.2)

  ちなみに、動物や植物の遺骸の年代測定に ¹⁴C という炭素の放射性同位体が使われているが、この半減期は約5730年。 ²³⁵U の核分裂によって生成されるセシウム (Ce) の放射性同位体 ¹³⁷Ce の半減期は約30.1年。

• 岩石のもつ発熱量は典型的には \(10^{-12}\) W/kg (ピコワット毎キログラム)、 最大で \(10^{-10}\sim10^{-9}\) W/kg 程度。(表8.3)
  個々の岩石でみればさほど大きくはないが、地球の全質量 (約 \(6\times10^{24}\) kg)・歴史 (約46億年) の間で合計すると、とても大きな発熱量になる。
• マントルと比べて地殻は非常に大きな発熱量をもつ。 (表8.3; 最大で約100倍)

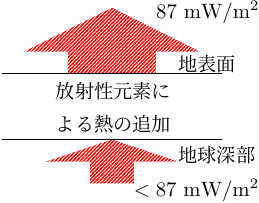
地殻熱流量について

(地殻熱流量) = (地殻の中にある放射性元素の発熱量) + (その下のマントルからやってくる熱流量)

という関係があるはずである。 ということは、地殻の中の発熱量が十分大きいなら、マントルからやってくる熱流量はもっと小さくてもよいので、マントル内の地温勾配がもっとゆるやかでもよいことになる。 しかし実際には、地殻熱流量 (平均約 87 mW/m²) のうち、地殻を構成している岩石に含まれる放射性元素からの発熱量はごくわずかしかない (その理由は、地殻の占める割合はとても小さいから)。

この議論によるとやはり、地殻熱流量のほとんどは地殻より下のマントルからやってきた熱であるということになってしまう。とはいえ、このような大量の熱が熱伝導によってマントルからやってくるとは考えにくい。 すなわち地球深部では、熱伝導よりももっと効率のよいメカニズムで熱を運んでいると考えるべきである。

そういえば最近は、ウランやトリウムが放射壊変する際に放出される「ニュートリノ」という素粒子が地球内部から飛び出してくる量を測定することで、地球が本当に持っている放射性元素の量を直接決めてやろう、なんていう試みも行われている。このような研究が進むと、この授業でも採用した「地球の平均的な組成は隕石とだいたい同じ」という (伝統的な) 仮定がどの程度正しいのかが検証できるようになるかも。

対流による熱輸送 (第10.4.3章)

伝導とは異なり、モノが移動することによって熱を運ぶしくみを「対流 (convection)」という。 モノの動きによって、そのモノが持っている熱エネルギーもいっしょに運ばれる というのが対流の仕組みである。

対流現象の例の1つとして、お椀の中のみそ汁などが挙げられる。 お椀の中のみそ汁の対流では、

• 表面で冷えたみそ汁が重くなって沈み、
• 底の温かいみそ汁が軽くなって浮いてくる

はずだが、このようなみそ汁の動きにより、お椀の中から外へと熱が運ばれている。

対流は、地球深部で熱を運ぶしくみとして非常に重要である。 詳細は後述するが、地球マントルの中で起こっているであろう対流の性質を考えれば、地殻熱流量の値を含めたいくつかの観測量をうまく説明することができる。