今回は「相関」とか「相関係数」の話。 テキスト第4章に沿って進める。
相関、相関係数
相関とは
変化する2つのデータの間に、
- 一方が増加したらもう一方も増加する (正の相関) 、あるいは
- 一方が増加したらもう一方は減少する (負の相関)
2つのデータの間によい相関があるならば、
- 相関の「強さ」を数字で測りたくなる。「相関係数」
- データどうしの間の関係を直線で「あてはめ」たくなる。
相関係数とは
ここで扱う相関係数は「線形相関係数 (linear correlation coefficient)」とも、「ピアソンの積率相関係数 (Pearson product-moment correlation coefficient)」とも呼ばれている。
\(N\) 個のデータの組 \((x_1, y_1),\cdots,(x_N,y_N)\) があるとき、相関係数 \(r\) は次のように定義される。 \begin{equation} r\equiv\dfrac{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\overline{x})^2}\sqrt{\dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(y_i-\overline{y})^2}} =\dfrac{\displaystyle\sum_{i=1}^{N}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\displaystyle\sum_{i=1}^{N}(x-\overline{x})^2}\sqrt{\displaystyle\sum_{i=1}^{N}(y-\overline{y})^2}} \tag{4.1} \end{equation} 定義式の各項はどういう意味か?
- 分母は \(x\) の標準偏差 \(\sigma_x\) と \(y\) の標準偏差 \(\sigma_y\) の積 \({\sigma_x}{\sigma_y}\) (当然)。
- 分子は \(x\) と \(y\) の「共分散 (covariance)」 とも呼ばれる。 \(\sigma_{xy}\) と書いたりする。
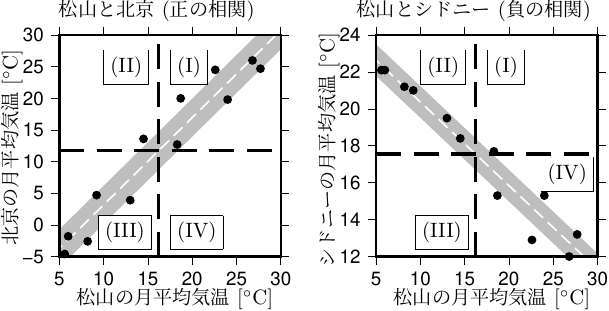共分散の意味を理解するため、分布を示すグラフを右図のように、\(\overline{x}\) と \(\overline{y}\) との大小関係で4つの部分に分けてみる (第1象限から第4象限に相当; 図4.2も参照)。
- 正の相関がある場合には、データのほとんどは (I) と (III) に分布
- \((x_i-\overline{x})(y_i-\overline{y})\) はほとんどが正 になる。
- 負の相関がある場合には、データのほとんどは (II) と (IV) に分布
- \((x_i-\overline{x})(y_i-\overline{y})\) はほとんどが負 になる。
分散 \(\sigma^2\) に2通りの計算式があったのと同様に、共分散 \(\sigma_{xy}\) にももう1つの計算式がある。 共分散の定義式を変形していくと \begin{equation} \dfrac{1}{N}\displaystyle\sum_{i=1}^{N}(x_i-\overline{x})(y_i-\overline{y}) =\overline{(xy)}-(\overline{x})(\overline{y}) \tag{4.5} \end{equation} という関係式を得る。 プログラミングで共分散を求めるには、この計算式を用いるとよい。 しかし、分散を求める場合と同様に、2つの式の使い分けも必要になる。
以上をまとめると結局、相関係数 \(r\) は次の式で求められることになる。 \begin{equation} r=\dfrac{\overline{(xy)}-(\overline{x})(\overline{y})}{{\sigma_x}{\sigma_y}} \tag{4.7} \end{equation}
線形最小二乗法との関係
第05回で出てきた「最小二乗法の決定係数」\(r^2\) ((3.20)式)と比較してやると、相関係数の2乗が決定係数 になっていることが分かる。
相関係数と決定係数の関係から、
- 相関係数は \(-1\le{r}\le1\) を満たす (\(0\le{r^2}\le1\) だから)
- \(r\) が \(\pm1\) に近いほど、回帰直線からのばらつきが小さい (「相関が強い」)
相関係数と回帰直線の傾きの間には \begin{equation} {a}={r}\dfrac{\sigma_y}{\sigma_x} \quad\leftrightarrow\quad {r}={a}\dfrac{\sigma_x}{\sigma_y} \tag{4.9} \end{equation} という関係がある。 これより、
- 相関係数が正ならば、回帰直線は右上がり (傾きが正)
- 相関係数が負ならば、回帰直線は右下がり (傾きが負)
- 回帰直線が点 \((\overline{x},\overline{y})\) を通ることを利用すれば、回帰直線の方程式は \begin{equation} y={r}\dfrac{\sigma_y}{\sigma_x}(x-\overline{x})+\overline{y} ={r}\dfrac{\sigma_y}{\sigma_x}x +\left(\overline{y}-{r}\dfrac{\sigma_y}{\sigma_x}\overline{x}\right) \tag{4.10} \end{equation} と書ける。
極端な場合での相関係数の例
- もし2つのデータが全く同じ (\(y_i=x_i\)) だったら、式(4.10) より \(r=1\)。 すなわち、自分自身との相関をとったら、相関係数は1。
- もし2つのデータが正反対 (\(y_i=-x_i\)) だったら、式(4.11) より \(r=-1\)。
- \(x\) と \(y\) の順番を入れ換えても同じ。
相関係数に関する補足
- 相関の強さは、相関係数の絶対値 \(|r|\) に基づいて、慣習的に以下のように表現される (表4.2も参照)。
0.7〜1 強い相関がある 0.4〜0.7 中程度の相関がある 0.2〜0.4 弱い相関がある 0〜0.2 ほとんど相関がない - 相関の強さは、\(r\) に比例している訳ではない。
例えば、
- 「\(r=0.8\) の相関の程度が、\(r=0.4\) の相関の程度より 強い」というのは正しいけれど、
- 「\(r=0.8\) の相関の程度が、\(r=0.4\) の相関の程度より 2倍強い」というのは間違い。
- 「相関の有無」と「因果関係の有無」は別物である。
例えば
- 「松山が暑い月」 は 「北京が暑い月」というのは正しいけれど、
- 「松山が暑い月」だから「北京が暑い月」というのは間違い。