今回は新たに「回帰 (regression)」とか「最小二乗法 (lease square method)」。 テキスト第3章に沿って進める。
回帰とは
2種類のデータ \(\{x_1,x_2,\cdots,x_N\}\) と \(\{y_1,y_2,\cdots,y_N\}\) の間の関係を調べたい。
- もし両者の間に線形な関係 (直線のグラフで表されるもの) があるはずならば、データをうまく「あてはめ」た直線を引きたくなる。 データをうまく「あてはめ」た直線の方程式を求めることを、線形回帰 という。
- 「あてはめ」る関係式は、直線でなくてもOK。 他には多項式、指数関数 (放射性元素の半減期とか) でもOK。
- あるいは、3種類以上のデータの間の関係式を調べるのもOK (「重回帰分析」)。
- 「あてはめ」に使う関係式の係数を求める方法の1つが最小二乗法。
線形最小二乗法
\(N\) 個のデータの組 \((x_1, y_1),\cdots, (x_N,y_N)\) があるとき、これを直線 \(y=ax+b\) に回帰させることを考える。
回帰直線の方程式を求める
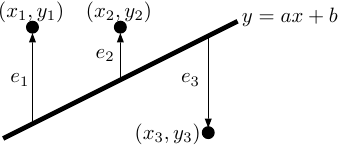
各々のデータ \((x_i,y_i)\) について、 \[ {e_i}\equiv{y_i}-{({a}x_i+b)} \tag{3.1} \] で定義される \(e_i\) を考えると、これは「あてはめ」られた直線 \(y=ax+b\) からのずれを表す量である (右図; 図3.1も参照)。
データの「あてはめ」の程度を、\(e_i\) の2乗の平均値 \(E\) (分散みたいなもの) により見積る。 その際、\(a\)、\(b\) をうまく選ぶことにより、\(E\) をできるだけ小さくしたい。 \begin{align} E& =\frac{1}{N}\sum_{i=1}^{N}(e_i)^2=\frac{1}{N}\sum_{i=1}^{N}(y_i-{a}x_i-b)^2 \notag\\& =\frac{1}{N}\sum_{i=1}^{N}{y_i}^2+{a}^2\frac{1}{N}\sum_{i=1}^{N}{x_i}^2+{b}^2-2{a}\frac{1}{N}\sum_{i=1}^{N}{x_i}{y_i}+2{a}{b}\frac{1}{N}\sum_{i=1}^{N}{x_i}-2{b}\frac{1}{N}\sum_{i=1}^{N}{y_i} \tag{3.2} \end{align} なお式変形にあたって、\(a\) と \(b\) は定数だから \(\sum\) の外に出せることを繰り返し用いている。 さらに、この中にある見覚えのある項を形式的に書き直すと、 \begin{equation} E=\overline{(y^2)}+{a}^2\overline{(x^2)}+{b}^2-2{a}\overline{(xy)}+2{a}{b}(\overline{x})-2{b}(\overline{y}) \tag{3.3} \end{equation} のようになる。
\(E\) が最小となるように \(a\) と \(b\) の値を決めたい (まさに「最小二乗法」)。 そこで \(E\) が極値をとるような \(a\) と \(b\) を探そう。 \begin{equation} \begin{split} 0&=\frac{\partial{E}}{\partial{a}} =2{a}\overline{(x^2)}-2\overline{(xy)}+2{b}(\overline{x}) \\ 0&=\frac{\partial{E}}{\partial{b}} =2{b}+2{a}(\overline{x})-2(\overline{y}) \end{split} \tag{3.4} \end{equation} これらを整理すると、\(a\) と \(b\) に関する連立一次方程式になる。 \begin{equation} \begin{split} {a}\overline{(x^2)}+{b}(\overline{x}) &= \overline{(xy)} \\ {a}(\overline{x})+{b} &= (\overline{y}) \end{split} \tag{3.5} \end{equation} これから \(a\) を解くと \begin{align} {a}& =\frac{\overline{(xy)}-(\overline{x})(\overline{y})}{\overline{(x^2)}-(\overline{x})^2} \tag{3.6} \\& =\frac{\overline{(xy)}-(\overline{x})(\overline{y})}{{\sigma_x}^2} \tag{3.7} \end{align} この \(a\) を使うと、\(b\) は次の式により求まる。 \begin{equation} b=\overline{y}-{a}\overline{x} \tag{3.9} \end{equation}
回帰直線の特徴
求める直線の方程式は \begin{equation} y={a}{x}+{b}={a}{x}+\overline{y}-{a}\overline{x} ={a}({x}-\overline{x})+\overline{y} \tag{3.16} \end{equation} この直線は常に点 \((x,y)=(\overline{x},\overline{y})\) を通るはず。 即ち回帰直線とは、例えば図3.2のように
- 1つの「固定点」\((x,y)=(\overline{x},\overline{y})\) を必ず通りつつ、
- 傾き \(a\) が「いい感じ」になるように (回帰直線とデータとの「ずれ」の指標 \(E\) が最小になるように)
「あてはめ」のもっともらしさ
ここで求まった \(a\) と \(b\) を使うと、「あてはめ」られた直線からのずれの二乗の平均 \(E\) はどのくらいに小さくなっているだろうか。 式(3.9)を利用して、もとの式を変形してみると \begin{equation} E={\sigma_y}^2-{a}^2{\sigma_x}^2 \tag{3.17} \end{equation} と書き直せる。 この式より、 \begin{equation} 0\le{E}\le{\sigma_y}^2 \tag{3.18} \end{equation} であることが分かる。 特に
- 求まった回帰直線の傾き \({a}=0\) ならば \(E={\sigma_y}^2\) であるし (当たり前)、
- また \({a}\not=0\) ならば必ず \(E<{\sigma_y}^2\)になる
ということは、「\(E\) がどれくらい小さくなったか?」を数字で表わすには、\(E\) と \(y\) の分散 \({\sigma_y}^2\) との比を調べるのが有効である。 \begin{equation} \frac{E}{{\sigma_y}^2}=1-{a}^2\frac{{\sigma_x}^2}{{\sigma_y}^2} \tag{3.19} \end{equation} であるが、この式に登場する \({a}^2\dfrac{{\sigma_x}^2}{{\sigma_y}^2}\) という項を \(r^2\) と書いてみることにしよう。 この \(r^2\) を 決定係数と呼び。 \begin{equation} r^2=a^2\dfrac{{\sigma_x}^2}{{\sigma_y}^2} =\left[\dfrac{\overline{(xy)}-(\overline{x})(\overline{y})}{{\sigma_x}^2}\right]^2\dfrac{{\sigma_x}^2}{{\sigma_y}^2} =\frac{\left[\overline{(xy)}-(\overline{x})(\overline{y})\right]^2}{{\sigma_x}^2{\sigma_y}^2} \tag{3.20} \end{equation} のように与えられる。
データ \(\{y_1,y_2,\cdots,y_N\}\) のばらつきを調べると、
- 平均値 \(\overline{y}\) からのばらつきが \({\sigma_y}^2\) (要するに「分散」そのもの)
- 回帰直線 \(y=ax+b\) による予測値からのばらつきが \(E={\sigma_y}^2(1-r^2)\)
- 平均値 \(\overline{y}\) から標準偏差 \(\sigma_y\) 1つ分 (通称 one sigma) の範囲内に、そこそこの割合のデータが含まれる (図3.3a; 正規分布なら約68%)。
- 回帰直線 \(y=ax+b\) による予測値から \(\sqrt{E}=\sigma_y\sqrt{1-r^2}\) 1つ分の範囲内にも、同じくらいそこそこの割合のデータが含まれる (図3.3b)。
\(0\le{E}={\sigma_y}^2(1-r^2)\le{\sigma_y}^2\) であることから、決定係数 \(r^2\) は \(0\le{r^2}\le1\) を満たす。
- \(r^2\) が 1 に近いほど回帰直線からの差が小さい (\(E\simeq0\)) ⇒ 「直線によるあてはめ」がうまくいっている
- \(r^2\) が 0 に近いほど回帰直線からの差が大きい (\(E\simeq{\sigma_y}^2\)) ⇒ 「直線によるあてはめ」をしてもうまくいかない
最小二乗法で「あてはめ」の計算をする際には、必ず決定係数の値もチェックすること。
- Excel で最小二乗法の計算をする際には、「グラフにR-2乗値を表示する」というチェックボックスにチェックをいれればOK。
- LibreOffice でも可能で、ソレ用の関数がちゃんと用意されている。
\(a\) = SLOPE(DataY;DataX) \(b\) = INTERCEPT(DataY;DataX) \(r^2\) = RSQ(DataY;DataX)