地震学入門 (その2): 地震の揺れの起こり方 (第2.1章)
震源断層 (第2.2.1章c)
地震波の発生源としての断層を「震源断層」という。
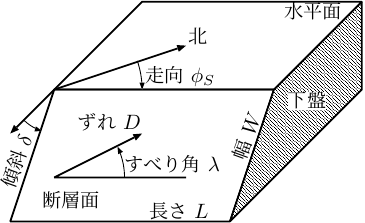震源となる断層のずれ方 (右図、図2.4も参照): どの向きの断層が、どうすべったか?
- 断層の面の方位は「走向 (strike)」 \(\phi_S\) と「傾斜 (dip)」 \(\delta\) で指定 (地質学で出てくるのと同じ)。
断層の面が水平面に対してどの方向にどれだけ傾いているか?を示している。
- 「走向」とは、断層面と水平面との交線が伸びる向き (ただし走向が大きくなる向きに断層が沈降するようにとる)。 地震学では「真北の向きとその交線の向きのなす角」を \(0^\circ\le\phi_S\le360^\circ\) で指定するのがふつう。
- 「傾斜」とは、断層面と水平面とがなす角。 \(0^\circ\le\delta\le90^\circ\) で指定する。
- すべりの向きは「すべり角 (rake)」 \(\lambda\) で指定。
下盤に対する上盤の動きの向きを \(-180^\circ<\lambda\le180^\circ\) で指定。
- \(\lambda=-90^\circ\) だと純粋な正断層
- \(\lambda=0^\circ\) だと純粋な左横ずれ断層
- \(\lambda=90^\circ\) だと純粋な逆断層
- \(\lambda=180^\circ\) だと純粋な右横ずれ断層
地震モーメント (第2.1.5章b+c)
断層すべりとしての地震の大きさを表わす物理量として、「地震モーメント (seismic moment)」 \(M_o\) が用いられる。 \begin{equation} M_o=\mu{D}{S} \tag{2.1} \end{equation} ただし \(\mu\) は岩石の剛性率 [Pa]=[N/m2]、\(D\) は断層のすべり量 [m]、\(S\) は断層の面積 [m2]。 これより、\(M_o\) の単位は [Pa × m × m2] = [J] となり、エネルギーと同じ単位を持っていることが分かる。 また定義から当然、地震モーメント \(M_o\) は断層のすべり量 \(D\) やすべった断層の面積 \(S\) が大きいほど大きい。
地震モーメントから換算された地震のマグニチュードを「モーメントマグニチュード (moment magnitude)」といい、次の式で計算される。 \begin{equation} M_w=\frac{1}{1.5}\left(\log_{10}{M_o}-9.1\right) \tag{2.2} \end{equation} 当然ながら、マグニチュードが2大きくなると、地震モーメントは \(10^3\) 倍になる。
地震波と発震機構 (第2.3章)
地震波の観測から、地震を起こした断層のずれを知るにはどうすればよいか? を考えてみる。
なお既に述べたように、地震とは「震源となる断層がずれる」ことによって起こるもののであるから、その起こり方を表現するには
- すべった断層の面の向き (断層面の法線の方向) と
- 断層がすべった向き
地震波を生みだす原動力: 二重偶力
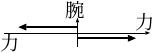
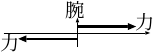偶力とは、大きさが同じで向きが反対の力の組み合わせのこと (右図; 図2.33a)。
力の作用点が「腕」の方向にずれている。
そのため、回転させようとする効果もある。
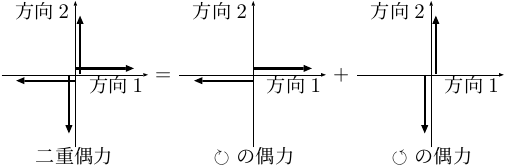直交する2組の偶力を組み合わせたものを二重偶力 (double couple) という (右図; 図2.33b)。
断層がずれたことによって生じる変位と地震波は、二重偶力によって生じるものと等しくなる (図2.37)。
偶力1つだけだと回転運動が生じてしまうが、それを打ち消すような2つめの偶力が合わさっている。
図2.33b のような二重偶力によって、どのような地震波が放出されるか? (図2.36) ここでは P 波の放射パターン (図2.36a) に注目し、しかも簡単のため
- 「押し」(⊕; 震源から離れる方向に押される) と
- 「引き」(⊖; 震源に近づく方向に引かれる)
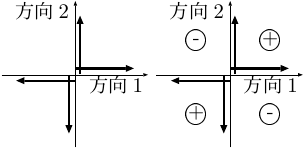4象限型のパターン:
直交する2つの「節面 (せつめん; nodal plane)」で 0、それらを境に「押し」と「引き」の領域が交互に現われる。
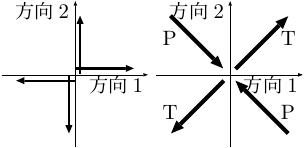(図2.37d)
偶力が外向きの方向を「T 軸」、内向きの方向を「P 軸」という。
震源は T 軸の方向に引っぱられ、P 軸の方向に圧縮されている。
実際の地震の記録でも、観測されるP波の初動の「押し」と「引き」の分布は4象限型になっている。 ここで得られる2つの節面のうちのどちらか1つが断層面に対応している (もう1つの節面はすべりの方向と直交する面に対応)。 しかし、2つの節面のうちどちらが本当の断層面かは地震波の放射パターンだけからは決められないので、余震や地殻変動の分布など他の情報も組み合わせて検討される。
震源メカニズム解 (第2.3.3章d)
P波の初動の「押し」「引き」の分布を広範囲で観測することにより、震源における断層面の向きとすべりの方向が推定できる。
| 横ずれ型 | 正断層型 | 逆断層型 |
|---|---|---|
 |  |  |
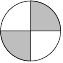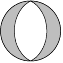この3次元的な分布を表現したものが震源メカニズム解にあたる。 右図のような「ビーチボール」で描き表わされ、以下のような手順で描かれている。
- 震源を中心とした仮想的な球面「震源球 (focal sphere)」の上に、P波の初動の「押し」「引き」の3次元的な分布を描く。 一般的には「押し」を色つきで、「引き」を白抜きで描く。
- 震源球の下半分にある面を水平面に投影して描く。