地球内部の「かたい」物質の「やわらかい」性質
地表のプレートを動かしているものは何か?
- Wegener の「大陸移動説」は、大陸を動かす力が説明できなかったせいで頓挫
- Holmes のマントル対流説により、大陸を動かす力が説明できたおかげで復活
では、「かたい」のに「やわらかい」とは、どういうことか?
地球内部での物質の変形のしかた (第10.2章)
「弾性 (elasticity)」と「粘性 (viscosity)」の2種類が重要。 ただし地球の表面に近い浅いところでは、「塑性 (plasticity)」も大事になってくる。
弾性とは
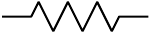簡単にいうと「ばね」の性質のことをいう (右図;図10.5a)。
地震波が伝わるのは、地球内部の物質に弾性的な性質があるおかげ。
- 力を加えると、即座に変形する。
力を取り去ると、もとの形に戻る。 - 加える力 \(F\) と、ばねの伸び \(x\) の間には
\begin{equation}
F=\overline{k}{x}
\tag{10.1}
\end{equation}
という比例関係がある (フックの法則)。
「かたい」ほど比例定数 \(\overline{k}\) は大きい。
力の単位は N (ニュートン)。1 ニュートンとは、質量が 1 kg の物体に 1 m/s2 の加速度を生じさせる力の大きさをいう。 1 [N] = 1 [kg] × 1 [m/s2]
- \(\overline{k}\) の単位は、ばねだと N/m、一般の物体だと N/m2 = Pa (パスカル; 圧力の単位と同じになる)
- もっと厳密には、2階のテンソルである応力 \(\boldsymbol{\sigma}\) と歪 (ひずみ) \(\boldsymbol{\varepsilon}\) の間の関係式として、4階の弾性テンソル \(C_{ijkl}\) を用いて \(\sigma_{ij}=C_{ijkl}\varepsilon_{kj}\) のように書かれる。
粘性とは
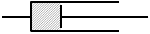流体が持っている、流れに抵抗する性質のことをいう。
「ダッシュポット」によく例えられる (右図;図10.5b)。
「ダッシュポット」とは、ピストンとシリンダーからなる振動減衰器のこと。例えば車やバイクでは、アクセルを急に放したとしても急激な振動が伝わらないようにするのに役立っている。
- 力を加えると、どこまでも変形しようとする。
力を取り去っても、もとの形には戻らない。 - 加える力 \(F\) と、ダッシュポットの伸びる速度 \(\dfrac{dx}{dt}\) の間には \begin{equation} F=\overline{\mu}\dfrac{dx}{dt} \tag{10.2} \end{equation} という比例関係がある。 「ねばねば」であるほど比例定数 \(\overline{\mu}\) は大きい。
- \(\overline{\mu}\) の単位は、ダッシュポットだと N/(m/s)、一般の物体だと (N/m2)s = Pa s (パスカル × 秒)
- もっと厳密には、2階のテンソルである応力 \(\boldsymbol{\sigma}\) と歪速度 \(\dot{\boldsymbol{\varepsilon}}\) の間の関係式として、粘性率 \(\eta\) を用いて \(\sigma_{ij}=\eta\dot{\varepsilon}_{ij}\) のように書かれる。 弾性とは異なり、粘性をテンソルで書くことはあまりない。それは単に、粘性率の「異方性」を考えた事例があまり多くないからであろうが。
塑性とは
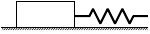例えば地震の際の断層のすべりなど。
摩擦のある床で物体を引っぱる場合にたとえられる (右図;図10.5c)。
- 加えた力が小さいうちは、力を取り去ったら元に戻る。
加えた力が大きくなると、力を取り去っても元に戻らない。
粘弾性とは
| マクスウェル粘弾性 |
|---|
 |
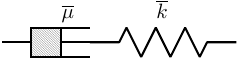- 現実の物質は、弾性と粘性の両方の性質「粘弾性 (viscoelasticity)」をもっている。 粘弾性的な性質を持っている物体を「粘弾性体」という。
- 粘弾性体の性質は、ばねとダッシュポットを組み合わせることによって表現される。
その例: マクスウェル粘弾性 (右図; 図10.6a)
ばねとダッシュポットが 直列に つながっている。
| フォークト粘弾性 |
|---|
 |
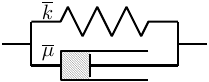ただし実際には、マクスウェル粘弾性の他にも粘弾性の性質を考えることができる。その1つの例として、ばねとダッシュポットが並列につながったものをフォークト (Voigt) あるいはケルビン (Kelvin) 粘弾性という。
ちょっと寄り道: 「変形のしかた」の話を「電気回路」の話と比べてみよう
ここで扱おうとしている弾性・粘性 (や粘弾性) の話は、高校 (や中学) の物理の授業で習った「電気回路」の話と実はよく似ている。
その実例として、「ばね」と「抵抗」の合成を考えてみる。 「直列」つなぎと「並列」つなぎで、それぞれどう求められたか? またそうなった根拠は何だったか?
直列つなぎ  | 並列つなぎ  | |
|---|---|---|
| ばね | 2つのばねの合成ばね定数は \(\displaystyle\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\) | 2つのばねの合成ばね定数は \(\displaystyle{k}={k_1}+{k_2}\) |
|
2つのばねにかかる力 \(F\) が同じで、全体の伸びはそれぞれのばねの伸びの和 よって \(\displaystyle{x}=x_1+x_2=\frac{F}{k_1}+\frac{F}{k_2}=\left(\textcolor{red}{\frac{1}{k_1}+\frac{1}{k_2}}\right){F}=\textcolor{red}{\frac{1}{k}}{F}\) |
2つのばねの伸び \(x\) が同じで、全体の力はそれぞれのばねにかかる力の和 よって \(\displaystyle{F}=F_1+F_2={k_1}{x}+{k_2}{x}=(\textcolor{red}{k_1+k_2})x=\textcolor{red}{k}{x}\) |
|
| 抵抗 | 2つの抵抗の合成抵抗は \(\displaystyle{R}={R_1}+{R_2}\) | 2つの抵抗の合成抵抗は \(\displaystyle\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\) |
|
2つの抵抗に流れる電流 \(I\) が同じで、全体の電圧はそれぞれの抵抗にかかる電圧の和 よって \(\displaystyle{V}=V_1+V_2={R_1}{I}+{R_2}{I}={R}{I}=(\textcolor{red}{R_1+R_2}){I}=\textcolor{red}{R}{I}\) |
2つの抵抗にかかる電圧 \(V\) が同じで、全体の電流はそれぞれの抵抗に流れる電流の和 よって \(\displaystyle{I}=I_1+I_2=\frac{V}{R_1}+\frac{V}{R_2}=\left(\textcolor{red}{\frac{1}{R_1}+\frac{1}{R_2}}\right){V}=\textcolor{red}{\frac{1}{R}}{V}\) |
| 電気回路でいうところの | 電圧 (電位差) \(V\) | が、物質の変形でいうところの | 伸び \(x\) | に対応していることが分かる。 |
| 電流 \(I\) | 力 \(F\) | |||
| 抵抗の逆数 \(1/R\) | ばね定数 \(k\) |
ちなみに、物質の変形でいうところのダッシュポットは、電気回路でいうところのコンデンサに対応している。 静電容量が \(C\) のコンデンサでは、蓄えられた電気量 \(Q\) と電極間の電位差 \(V\) の間に \(Q=CV\) という関係があったはず。 さらに、コンデンサを流れる電流 \(I\) が \(I=\displaystyle\frac{dQ}{dt}\) で与えられることから、結局 \(I=C\displaystyle\frac{dV}{dt}\) という関係式が得られる。
マクスウェル粘弾性体のふるまい
マクスウェル粘弾性体のふるまいは、「マクスウェル時間」 \(\tau_{ve}\equiv{\overline{\mu}}/\overline{k}\) と比べて どれくらい長い時間をかけて観察するか? によって異なる。 「マクスウェル時間」と比べて
- 短い時間スケール では、弾性的 なふるまいが目立つ。
- 長い時間スケール では、粘性的 なふるまいが目立つ。
- 伸びを与えた直後では、ばねの伸び \(x_e\) は大きいけれど、ダッシュポットの伸び \(x_v\) は小さい。
- ばねを大きく伸ばすために、大きな力がかかっている (式(10.1)参照)。
- 大きな力がかかっているので、ダッシュポットの伸びる速さは大きい (式(10.2)参照)。
- しかし時間の経過とともにダッシュポットの伸び \(x_v\) が大きくなると、ばねの伸び \(x_e\) が小さくなる。
- ばねの伸びが小さくなると、かかっている力も小さくなる。
- かかっている力が小さくなると、ダッシュポットの伸びる速さも小さくなる。
なお同じことは (非現実的な設定ではあるものの)、マクスウェル粘弾性体に一定の力 \(F\) をかけ続けた場合に、粘弾性体の伸び \(x\) の時間変化を調べてみることによっても理解できる (図10.7参照)。
地球マントルの弾性・粘性・粘弾性
地球のマントルにも粘弾性の性質がある。
- 地震の波が伝わる → 弾性
- 流れる → 粘性
マントル物質の弾性・粘性は、地球物理学データからも見積ることができる。 これらに基づくと、マントル物質のマクスウェル時間 \(\tau_{ve}\) はだいたい数百年〜数千年くらいになる。 よって、
- 数千年以上をかけて地球内部で起こる現象には、物質の粘性が重要
- それより短い時間スケールで起こる現象には、物質の弾性が重要