固体地球物理学概論 (2024年前学期) 第02回

ジオイド、正規重力 (第7.1章、7.2章)

ちょっとその前に: 保存力とポテンシャル

ポテンシャルとは、高校の物理でいうところの「位置エネルギー」のこと。 その力の方向に物体を動かすのに必要な仕事が、始点と終点だけで決まり、途中の経路によらないような力は「保存力」と呼ばれ、「保存力」には「ポテンシャル」が存在する。 その物理的な意味は次のようなものである。

1. ポテンシャルが一定の面は力の向きと垂直であるし、
2. ポテンシャルを空間の座標で微分したら力になる。

なお、微分が積分の逆にあたることを考えれば、2つめの点は「力を空間の座標で積分したらポテンシャルになる」と言い換えられる。

高校の物理で登場する好例の1つは、重力がはたらいている場の中で、物体を持ち上げる際の「位置エネルギー」の変化である (右図参照)。 このとき、物体の「位置エネルギー」は

• 重力 (と反対) の方向に移動した距離の分だけ大きくなり、しかも
• その変化量は、物体がどのような経路で移動したかによらずに決まる

という性質があったはず。 また、重力と垂直な方向にどれだけ移動しても「位置エネルギー」は変わらないのだから、「位置エネルギー」が一定の面は重力の方向と垂直になっていることもいえる。

重力ポテンシャル

万有引力と遠心力のそれぞれにポテンシャルが存在する。 万有引力のポテンシャルを\(V\)、遠心力のポテンシャルを\(U\)とかくと \begin{align} V(r)&=-G\frac{Mm}{r} \tag{7.5} \\ U(r)&=\frac{1}{2}m{r^2}\omega^2\cos^2\phi \tag{7.15} \end{align}

重力ポテンシャル \(W\) は両者の和であり \begin{equation} W=V+U=-G\frac{Mm}{r}+\frac{1}{2}m{r^2}\omega^2\cos^2\phi \tag{7.16} \end{equation}

繰り返すが、この式はごく理想的な場合でのみ成り立つものであり、現実は

• 地球の形が厳密な球ではない
• 地球の内部の密度の分布が球対称ではない

ことなどによって \(V\) の表式がもっと複雑なものになり、重力ポテンシャル \(W\) や重力 \(g\) の表式も変わってくる。 例えば地球の形が回転楕円体であることを考えてやった場合には、 \begin{equation} \begin{split} g&=G\frac{Mm}{r^2} -\frac{3GMm{R_e}^2{J_2}}{2r^4}(3\sin^2\phi-1) -m{r}\omega^2\cos^2\phi \\ W&=-G\frac{Mm}{r} +\frac{GMm{R_e}^2{J_2}}{2r^3}(3\sin^2\phi-1) +\frac{1}{2}m{r^2}\omega^2\cos^2\phi \end{split} \tag{7.29} \end{equation} と表わされる。 ここで \(R_e\) は赤道半径、\(\phi\) は緯度である。 また、新たにつけ加えられた右辺第2項に含まれている \(J_2\) は「力学的形状係数」などと呼ばれ、地球の形が回転楕円体である効果 (赤道まわりと極まわりの慣性モーメントの違い) を表わす無次元量である。

地球楕円体・ジオイド (第7.3章)

地球楕円体

地球の形は回転楕円体に近いはずだから、重力から地球の形を決める際にも、回転楕円体が作る重力を基準に考えるのがよい。 そこで用いられるのが「地球楕円体」である。 地球楕円体の表面では、自転する回転楕円体による重力のポテンシャル \(W\) ((7.29)式) が一定になっている。(その場所の重力の方向と垂直)

ジオイド

「ジオイド」とは、実際の地球で測定された重力のポテンシャルが一定になる面 (等ポテンシャル面) の1つで、地球楕円体の作る重力の等ポテンシャル面とよく一致するもののこと。

もちろんジオイドと地球楕円体は完全には一致しない。 地球楕円体に対するジオイドの起伏を「ジオイド高」という。 地球全体でみても、ジオイド高はたかだか \(\pm100\) m くらいで、地形の変化 (\(\pm10000\) m) と比べてかなり小さい。 このことからジオイド面が「高さ」を測る基準の1つとして使われていて、ジオイドから測った高さが「標高」である。

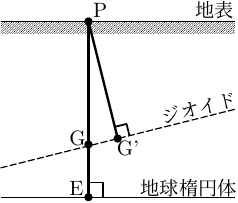
例えばジオイドと地球楕円体 (と地表) の位置関係が右図のようになっている場合について、地表面にある点Pの「高さ」に関する量として以下のものが定められる。

• EG を点Pにおける「ジオイド高」という。
• G'P を点Pの「標高」という。 (GP はジオイドと直交してないから、「高さ」にならない)
• EP を点Pの「楕円体高」という。 GPS で表示される「高さ」はこれ。

ジオイドの凸凹は、地形の凸凹や、地下にある物質の質量の分布に関係している。

地球の形と正規重力 (第7.4章)

地球の形を数式で表わそうとするならば、やはり回転楕円体にしたい (それが「地球楕円体」)。 そのような「地球のモデル」が作る理論的な重力を「正規重力」という。 観測の進歩により、地球楕円体を指定する量の値もどんどん「バージョンアップ」されている。 以下では「測地基準系1980」による地球楕円体 GRS80 を例にとって考える。

自転する回転楕円体のつくる重力の分布を決めることを考えよう。 緯度 \(\phi\) の場所にある質量 \(m\) の物体が受ける重力 \(g\) や重力ポテンシャル \(W\) が(7.29)式で与えられることを考えれば、以下の4つの量を指定してやればよいことが分かる (値は式(7.52)も参照)。

• 赤道半径 \(a=6,378.137\) [m] (式(7.29) でいうところの \(R_e\))
• 地心引力定数 \(GM=3,986,005\times10^8\) [m³/s²]
• 力学的形状係数 \(J_2=108,263\times10^{-8}\)
• 自転角速度 \(\omega=7,292,115\times10^{-11}\) [s^-1]

これらは「ストークス定数」あるいは「定義定数」などと呼ばれる。

回転楕円体の性質を考えれば、正規重力の値も緯度によってのみ決まり、経度にはよらない。 測地基準系1980による正規重力の値 \(\gamma_\phi\) の式として正式なものは \begin{equation} \gamma_\phi=\dfrac{a{\gamma_e}\cos^2\phi+b{\gamma_p}\sin^2\phi}{\sqrt{a^2\cos^2\phi+b^2\sin^2\phi}} \tag{7.53} \end{equation} で与えられる。 ここで \(b\) は地球の極半径、\(\gamma_e\) と \(\gamma_p\) はそれぞれ赤道と極における正規重力の値であり、これらの値は式(7.54) (そのうち \(\gamma_e=978.0\) Gal、\(\gamma_p=983.2\) Gal) を、また緯度 \(\phi\) による正規重力 \(\gamma_\phi\) の変化は図7.9を参照。 この式の精度は \(10^{-4}\) mGal である。 ただし実際には、この式を簡略化した \begin{equation} \gamma_\phi^\text{1980}=978.0327 \left(1+0.0053024\sin^2\phi -0.0000058\sin^2{2\phi}\right) \text{[Gal]} \tag{7.56} \end{equation} が用いられることが多い。 これは(7.53)式に「チェビシェフ近似」というものを施して得られたものだそうで、精度は\(0.1\) mGal 程度。

重力異常と重力補正 (第7.5章)

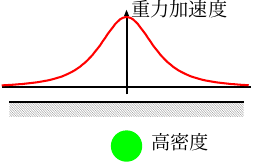
重力を測定する目的の1つは、地下の構造やその時間変化を知ることにある。 よくある例では、重力加速度の大きさが場所ごとに違うことをうまく利用すると、地下にある物質の質量 (正確には密度) の違いを推定することができる。 なぜなら、地下にある物質の質量の違いによって引っぱられる力の大きさが違ってくる (右図参照) ことを考えると、

• 地下に重い (密度の高い) 物質があるところでは、その真上での重力加速度は大きくなる
• 地下に軽い (密度の低い) 物質があるところでは、その真上での重力加速度は小さくなる

はすだからである (ただし、地球全体の規模で考えると、話はもう少し複雑になる)。 このような技術は、地下の異常な構造 (断層とかカルデラとか) や金属鉱床の存在を知る手掛かりとして重要である。

そのためには重力の観測値と基準値からのずれである「重力異常」を調べることになる。 重力の「異常」として最初に思いつくのは、正規重力 \(\gamma_\phi\) と比べた異常であろう。 しかしこの重力異常には、地下の構造の影響だけでなく、さまざまな仕組みによる影響が混じり込んでしまっている。 そのため、重力によって地下の構造を調べるには、観測された重力の値にさまざまな補正を加える必要がある。 概念的には図7.10を参照。

フリーエア補正

重力を測定した地点の標高 (ジオイド面からの高さ) が必ずしも0でないことの影響を補正するのが「フリーエア補正」。 これにより、測定された重力の値を、重力ポテンシャル \(W\) が一定の面であるジオイド面における重力の値に作り換える。図7.10(d)参照。 フリーエア補正を施した後の重力異常を「フリーエア異常」という。

万有引力の効果のみを考えると、標高 (\(\simeq\) 地球の中心からの距離) が \(1\) m 高くなれば、重力加速度はおよそ \(0.3086\) mGal 小さくなる (「フリーエア勾配」)。 よって、標高 \(h\) [m] の場所で重力観測を行う場合、\(0.3086\times{h}\) [mGal] を測定値に加える。

ブーゲー補正

ある標高の地点で測定された重力の値には、測定した地点とジオイド面の間に存在するはずの岩石がつくる引力の影響が含まれているはず。 この影響を除去しようとするのが「ブーゲー補正」。

ブーゲー補正にはいろいろなやり方があるが、最も簡単なものは \begin{equation} {BC}_i=2\pi{G}{\rho}{h} \tag{7.63} \end{equation} とする方法である。 これは厚さ\(h\)で密度\(\rho\)をもち、水平方向に無限に伸びた平板 (図7.10(c)) が、平板上の点に及ぼす引力である。 密度\(\rho\) として \(\rho=2.67\) g/cm³ とすると、標高 \(h\) [m] の地点で重力観測を行う場合には \begin{equation} {BC}_i=0.11194\times{h} \text{[mGal]} \tag{7.64} \end{equation} を測定値から引く。 またフリーエア補正とブーゲー補正を合わせると、 \begin{equation} 0.3086\times{h}-0.11194\times{h}=0.19666\times{h} \text{[mGal]} \tag{7.65} \end{equation} となる。 この補正を「単純ブーゲー補正」という。 地形の起伏が小さい場合には単純ブーゲー補正で十分だが、そうでない場合にはもう少し複雑な補正が必要になる。 例えば

• 有限平板の効果: 平板が無限には広がっていない効果
• 有限球殻の効果: 地球がまるい効果

を考えてやる必要がでてくる。

地形補正

観測地点を含む地形がジオイド面と比べて凸凹している効果を補正してやる。

地形補正を施すには、コンピュータの中で実際の地形を仮想的に再現し、補正量を計算することになる。 ただし計算を簡略化するために、地形を2次元の「扇型」や「角柱」に分割して近似し、それらによる効果を足し合わせる、ということもよく行われている。