地球の重力、地球のかたち
重力とは (第7.1章)
重力とは、物体が地球から受ける力のこと。
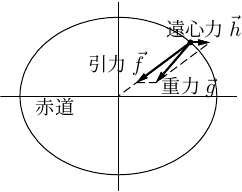
右図 (教科書の図7.1と同じ) より、
重力 \(\vec{g}\) = 地球の質量による万有引力 \(\vec{f}\) + 地球の自転による遠心力 \(\vec{h}\)力はベクトルなので、向きと大きさをもつことに注意せよ。 上の式の力の足し合わせも、ベクトルの足し算として行われている。
物体にはたらく重力は、その物体の質量に比例する。 単位質量 (1 kg) あたりにはたらく重力を「重力加速度」という。 よく言われる重力加速度の大きさは \(g=9.8\) m/s2。
- 物理学の分野ではふつう加速度の単位として m/s2 (メートル毎秒毎秒) を用いるが、地球科学の分野 (の一部) では重力加速度の単位として Gal「ガル」を使うことが多い。 1 Gal = 0.01 m/s2 = 1 cm/s2 (センチメートル毎秒毎秒)
- ただし、重力加速度のわずかな変化をみる際には、 mGal「ミリガル」(千分の1 Gal) や μGal 「マイクロガル」(百万分の1 Gal) がよく使われる。
以下では主に、質量 \(m\) の物体にはたらく重力を考える。
万有引力による寄与 (第7.1章、7.2章)
すべての物体の間には、互いに引き合う力がはたらく。
この力を「万有引力」とよぶ。
万有引力の大きさは、2つの物体の質量の積に比例し、2つの物体の間の距離の2乗に反比例する。
これは「ニュートンの万有引力の法則」とよばれるもので、数式では
\begin{equation}
f=G\dfrac{Mm}{r^2}
\tag{7.1}
\end{equation}
のように書かれる。
(7.1) に登場する比例定数 \(G\) を万有引力定数といい、\(G=6.67259\times10^{-11}\) m3/kg/s2 である。
この万有引力は、ふだんの生活の中では感じられないほど小さい。例えば、1 m だけ離れたところにある 100 kg の物体から受ける万有引力の大きさは、地球から受ける重力の約15億分の1である。
地球の質量による万有引力を見積ってみよう。 話を簡単にするため、地球を質量 \(M_e\)、半径 \(R_a\)の完全な球と仮定する。 しかも地球の内部での密度の分布は球対称 (中心からの距離 \(r\) だけで決まる) という理想的な場合を考える。 このとき、地球の中心から \(r\) の距離にある質量 \(m\) の物体が、地球から受ける万有引力 \(\vec{f}\) の大きさはいくらか?
- 地球の表面および外部 (\({r}\ge{R_a}\)) では、 \[ f(r)=G\frac{{M_e}m}{r^2} \tag{7.43} \] すなわち、地球の全質量が中心に集中したと思ったときに生じる万有引力と等しい。
- 地球の内部 (\({r}<{R_a}\)) では \[ f(r)=G\frac{{M_r}m}{r^2} \tag{7.42} \] ただし \(M_r\) は、地球の中心から半径 \(r\) の球の部分にある質量。 すなわち、自身のいる位置 \(r\) より内側にある質量による万有引力のみを受け、自身より外側にある部分からの影響はない。
なぜこうなるかは、地球の内部を「薄っぺらい球殻」の積み重ねで考えると理解できる。 数式できっちりと証明するのはけっこう大変 (興味のある人は第7.2.1章を参照のこと) なんだが、その概略はだいたい以下のような感じになっている。 ただしここでも、力の足し算はベクトルとして実行されることに注意!!
- 物体が球殻の外側にある場合 (図7.4)
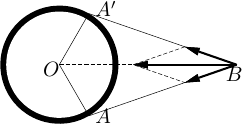
球殻上の点 \(A\) にある部分が点 \(B\) に及ぼす引力と、 点 \(A'\) にある部分が点 \(B\) に及ぼす引力とを足すと、地球の中心を向く力ができる。 これを球殻全体に広げて考えればよい。 - 物体が球殻の内側にある場合
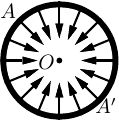
簡単のため球殻の中心 \(O\) にはたらく万有引力について考える。 球殻上の点 \(A\) にある部分が点 \(O\) に及ぼす引力と、その正反対の位置にある点 \(A'\) にある部分が点 \(O\) に及ぼす引力とを比べると、この2つは同じ大きさで向きが反対だから、2つの力の合力は0になる。 同じことは球殻上の他の点についてもいえるから、球殻全体から受ける力の合計は0になる。 中心でない点でも同様に成り立つ。
個々の「薄っぺらい球殻」で成り立つから、これらを積み重ねた球全体でも成り立つ。
以上のことにより、地球 (を含めた天体) の外側における重力加速度は、その天体の中心からの距離の2乗に反比例して小さくなる ことがいえる。
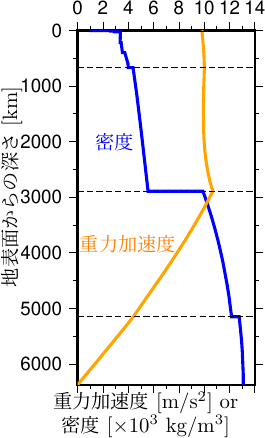
これに対して、天体の内側における重力加速度の分布を知るには、その天体の内部での密度の分布を知る必要がある。 例えば PREM (Preliminary Reference Earth Model) による地球内部の密度の分布に基づくと、地球内部の重力加速度の分布は図7.6のように見積もることができる (右図も参照)。 この図より、地球内部の重力加速度の分布の特徴として
- 中心に近い核の中では、地球の中心からの距離にほぼ正比例して増加
- 核より外側にあるマントルや地殻の中では、地球の中心からの距離によらずほぼ一定
遠心力による寄与 (第7.1.2章)
等速円運動している質量 \(m\) の物体にはたらく遠心力 \(\vec{h}\) の大きさは \[ h=mr\omega^2 \tag{7.12} \] で与えられる。 ただし \(r\) は回転半径 (万有引力のときに出てきた \(r\) とは別物)、\(\omega\) は回転の角速度で、回転の周期 \(T\) を用いて \[ \omega=\frac{2\pi}{T} \tag{7.13} \] で与えられる。 なお (7.13) に限らず物理学の世界では一般に、角度を「度」ではなく「ラジアン (radian)」ではかることに注意。 地球が「1日で自転する」ということは、「24時間=(60×60×24) 秒の間に360°=\(2\pi\) ラジアンだけ回転している」ということだから、地球の自転による角速度は \[ \omega=\frac{2\pi\text{[rad]}}{60\times60\times24\text{[s]}}=7.272\times10^{-5} \text{[rad/s]} \tag{7.17} \]
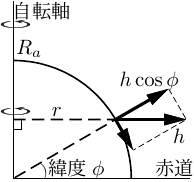地球の自転による遠心力を考えると、
緯度が \(\phi\) の地点での回転半径 (自転軸からの距離) は \(r={R_a}\cos\phi\) だから、この地点にはたらく遠心力の大きさは \(h=m{R_a}\omega^2\cos\phi\)。
特に、遠心力のうち外側 (万有引力と反対の向き) にはたらく分力の大きさは
\(h\cos\phi=m{R_a}\omega^2\cos^2\phi\) となる。
遠心力が最も強くはたらく赤道 (緯度 \(\phi=0\)) において、地球の万有引力と遠心力の比をとると、 \begin{equation} \frac{G\dfrac{M_e{m}}{{R_a}^2}}{m{R_a}\omega^2} =\frac{G\dfrac{M_e}{{R_a}^2}}{{R_a}\omega^2} =\frac{9.8\text{[m/s$^2$]}}{6.378\times10^6\text{[m]}\times(7.272\times10^{-5}\text{[rad/s]})^2} \simeq290 \tag{7.21} \end{equation} これより、遠心力の効果を考えただけで、地球の重力は緯度によって約 \(1/300=0.3\) % 変化することになる。
ただし実際には、遠心力の効果だけでなく、「地球が赤道方向につぶれている」効果も加わることにより、赤道での重力は極での重力と比べて 0.5% 程度小さい (詳しくは次回)。 また「低緯度のところほど重力が小さい」がゆえに、ロケットの発射基地はできるだけ赤道に近い場所にあったほうが好都合だということになる。