第02回で「平均・分散・標準偏差」の定義などの説明はざっくり終わっている。 しかし (演習の進度との調整を例年やっている都合もあり)、平均とか分散とか標準偏差に関連した話を2回分入れておきたい。 その1回目は、テキスト第2章の前半に沿って、確率とか正規分布とかの話をする。 次回は誤差論の入口の話をする予定であるので、そのきっかけになりそうな感じで。
「確率」と「平均」の関係
「平均」とは、確率の言葉でいえば「期待値」のこと。 これをいま一度ふり返ってみる。
- いま \(N\) 個のデータ \(\{y_1,y_2,\cdots,y_N\}\) があるとする。
その平均値を \(\overline{y}\) とかくと、
\begin{equation}
\overline{y}
=\frac{y_1+y_2+\cdots+y_{N-1}+y_N}{N}
={y_1}\frac{1}{N}+{y_2}\frac{1}{N}+\cdots+{y_N}\frac{1}{N}
\tag{2.1}
\end{equation}
このうち \(\dfrac{1}{N}\) は、 \(N\) 個のデータからその1つを選んでくる確率のこと。
- 具体例は、前回にやった「1年間の平均気温」。 \begin{equation} \fbox{年平均気温}=\fbox{1月の平均気温}\times\frac{1}{12} +\cdots+\fbox{12月の平均気温}\times\frac{1}{12} \tag{2.2} \end{equation} このうち \(\dfrac{1}{12}\) は、12ヶ月のうちからある1ヶ月が選ばれる確率のこと。 この場合、どの月が選ばれる確率も等しいと仮定されている。
- 年平均気温をもう少し正確に求めようとすれば、 \begin{equation} \fbox{年平均気温}=\fbox{1月の平均気温}\times\frac{31}{365} +\cdots+\fbox{12月の平均気温}\times\frac{31}{365} \tag{2.3} \end{equation} このうち \(\dfrac{31}{365}\) などは、365日のうち、その月の中の日が選ばれる確率のこと。
確率が一定でないことをとり入れた平均が「重みつき平均」である。 ここで登場する「重み」は「確率」であるからには、「重み」は全て正であり、また総和は1でなければならない。
図2.1と図1.1のグラフの違い、あるいは式(1.4)と式(2.6)との違いに注意。 図2.1では各月を表わす区間の幅は (実は) 一定ではない。 こうした区間の幅の違いを考慮した上で「平(たいら)に均す(ならす)」のが重みつき平均である。
平均・分散・標準偏差が出てくる例: 偏差値
偏差値 (へんさち、Standard score) とは、ある数値が母集団の中でどれくらいの位置にいるかを表した無次元数。
- いま \(N\) 個のデータ \(\{y_1,y_2,\cdots,y_N\}\) があるとする。 その平均を \(\overline{y}\) 、標準偏差を \(\sigma_y\) とかくと、各データの偏差値 \(T_i\) は以下で与えられる。 \begin{equation} T_i=\frac{10(y_i-\overline{y})}{\sigma_y}+50 \tag{2.7} \end{equation}
- 偏差値の性質: 平均値が50、標準偏差が10。 そうなるように式(2.7)は作られている。
表2.1のように、「偏差値の値が○以上だと上位△%」などとよく言われる。 ただしこれは、値の分布が「正規分布」に近いときのみ有効。
正規分布
ガウス関数
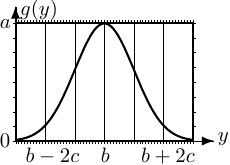
- ガウス関数 (Gaussian function) とは
\begin{equation}
g(y)=a\times\exp\left[-\dfrac{(y-{b})^2}{2{c}^2}\right]
\tag{2.10}
\end{equation}
のような形をした関数。
正規分布を表す関数もその1つ。
その形を図2.2に示す (右図も参照)。
- \(y={b}\) を中心にした「つりがね」型
- \(y={b}\) で極大、そこから離れると減少
- \(y={b}\) に関して対称
- \({c}\) が大きいほど「すそ」が広い
- ガウス関数は、地球科学に限らず、物理っぽい場面の多くで出てくる。
- スペクトル解析 (「ラマン分光」でスペクトルのピークのあてはめ)
- データの平滑化 (フィルタリング) などにも
- ガウス関数の性質
- \(y={b}\) で極大値 \(g(y={b})={a}\)
- \(y={b}\pm{c}\) で変曲点。 \(|y-{b}|<{c}\) のときグラフは上に凸。
- \(g(y)={g(y={b})}\times\dfrac{1}{2}\) となるのは、 \[ \exp\left[-\dfrac{(y-{b})^2}{2{c}^2}\right]=\dfrac{1}{2} \quad\Rightarrow\quad {y-{b}}=\pm{c}\sqrt{2\ln2} \simeq1.177{c} \tag{2.14} \] ただし \(\ln\) は自然対数 (底が10ではなく \(e\) のもの)。 これより \(2{c}\sqrt{2\ln2}\) を「半値全幅」 (FWHM; full width at half maximum)、あるいは単に「半値幅」と呼ぶ。
- もし無限回の測定ができた (例えば「無限大の人数がテストを受けた」) とすれば、測定値 (例えば「テストの点数」) の度数分布図 (ヒストグラム) は \begin{equation} G(y)=\frac{1}{\sqrt{2\pi}\sigma_y}\exp\left[-\frac{(y-{Y})^2}{2{\sigma_y}^2}\right] \tag{2.25} \end{equation} という形で表される正規分布になるはず。
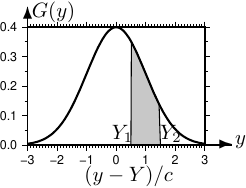その形を図2.3に示す (右図も参照)。
図2.3の影つきの部分の面積 \(\displaystyle\int_{Y_1}^{Y_2}G(y)dy\) は、測定値 \({y}\) が \({Y}_1\) と \({Y}_2\) の間にある確率を表わす。
あるいは (似たようなものだが)、 \({Y}_1\) と \({Y}_2\) の範囲の値が測定される確率を表わす。
- \(G(y)\) を \(-\infty\) から \(\infty\) の区間で積分すると1になる。 これは「確率」であることを考えれば当然。 \(\dfrac{1}{\sqrt{2\pi}\sigma_y}\) という係数はこのためについている。
- 正規分布をしている場合には、平均値から
- 標準偏差1つ分 (通称「one sigma」) の範囲に入っているデータの割合は 0.6827 (偏差値が40〜60の人は全体の約68%)
- 標準偏差2つ分 (通称「two sigma」) の範囲に入っているデータの割合は 0.9545 (偏差値が30〜70の人は全体の約95%)
- 標準偏差3つ分 (通称「three sigma」) の範囲に入っているデータの割合は 0.9973 (偏差値が20〜80の人は全体の約99.7%)
誤差関数
- 正規分布やガウス関数と関係して、「誤差関数」 \(\text{erf}\) が定義される。
\begin{equation}
\text{erf}(z)=\frac{2}{\sqrt{\pi}}\int_{0}^{z}\exp(-t^2)dt
\tag{2.30}
\end{equation}
定義式中で \(z\ge0\) かつ \(t=\dfrac{y-Y}{\sqrt{2}\sigma_y}\) だとみなすと、
\[
\begin{split}
\text{erf}(z)&
=\frac{2}{\sqrt{\pi}}\int_{Y}^{Y+\sqrt{2}{z}\sigma_y}\exp\left[-\frac{(y-Y)^2}{2{\sigma_y}^2}\right]\frac{dy}{\sqrt{2}\sigma_y}
\notag\\&
=2\int_{Y}^{Y+\sqrt{2}{z}\sigma_y}\frac{1}{\sqrt{2\pi}\sigma_y}\exp\left[-\frac{(y-Y)^2}{2{\sigma_y}^2}\right]{dy}
\end{split}
\]
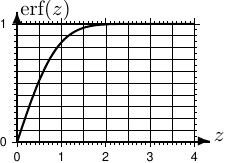この表式と、正規分布を表わすガウス関数 \(G(y)\) の表式(2.25)とを見比べると、
\begin{align}
\text{erf}(z)&
=2\int_{Y}^{Y+\sqrt{2}{z}\sigma_y}G(y){dy}
\tag{2.31}
\\&
=\int_{Y-\sqrt{2}{z}\sigma_y}^{Y+\sqrt{2}{z}\sigma_y}G(y){dy}
\tag{2.32}
\end{align}
\(y-Y\) は測定値 \(y\) の誤差 (「真の値」 \(Y\) からのずれ) に相当することから、 \(\text{erf}(z)\) は 「誤差」の大きさが \(\sqrt{2}{z}\sigma_y\) 以下である確率 ( \(-\sqrt{2}{z}\sigma_y\le{y-Y}\le\sqrt{2}{z}\sigma_y\) ) を表す。
- 誤差関数はこの他にも、いくつかの場面で登場する。 地球科学では、海洋プレートの年代と厚さの変化を見積る場合などに出てくる。